题目内容
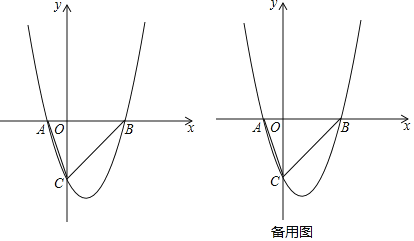
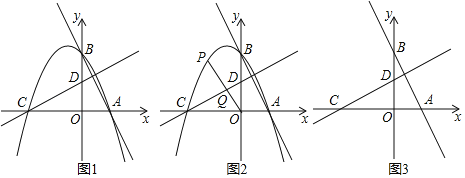
【题目】如图1,在平面直角坐标系中,直线AB:y=kx+b(k<0,b>0),与x轴交于点A、与y轴交于点B,直线CD与x轴交于点C、与y轴交于点D.若直线CD的解析式为y=﹣![]() (x+b),则称直线CD为直线AB的”姊线”,经过点A、B、C的抛物线称为直线AB的“母线”.
(x+b),则称直线CD为直线AB的”姊线”,经过点A、B、C的抛物线称为直线AB的“母线”.
(1)若直线AB的解析式为:y=﹣3x+6,求AB的”姊线”CD的解析式为: (直接填空);
(2)若直线AB的”母线”解析式为:![]() ,求AB的”姊线”CD的解析式;
,求AB的”姊线”CD的解析式;
(3)如图2,在(2)的条件下,点P为第二象限”母线”上的动点,连接OP,交”姊线”CD于点Q,设点P的横坐标为m,PQ与OQ的比值为y,求y与m的函数关系式,并求y的最大值;
(4)如图3,若AB的解析式为:y=mx+3(m<0),AB的“姊线”为CD,点G为AB的中点,点H为CD的中点,连接OH,若GH=![]() ,请直接写出AB的”母线”的函数解析式.
,请直接写出AB的”母线”的函数解析式.
【答案】(1)![]() ;(2)(2,0)、(0,4)、(﹣4,0);(3)当m=﹣
;(2)(2,0)、(0,4)、(﹣4,0);(3)当m=﹣![]() ,y最大值为
,y最大值为![]() ;(4)y=x2﹣2x﹣3.
;(4)y=x2﹣2x﹣3.
【解析】
(1)由k,b的值以及”姊线”的定义即可求解;
(2)令x=0,得y值,令y=0,得x值,即可求得点A、B、C的坐标,从而求得直线CD的表达式;
(3)设点P的横坐标为m,则点P(m,n),n=﹣![]() m2﹣m+4,
m2﹣m+4,
从而求得直线OP的表达式,将直线OP和CD表达式联立并解得点Q坐标,
由此求得![]() ,从而求得y=﹣
,从而求得y=﹣![]() m2﹣
m2﹣![]() m+3,故当m=﹣
m+3,故当m=﹣![]() ,y最大值为
,y最大值为![]() ;
;
(4)由直线AB的解析式可得AB的“姊线”CD的表达式y=﹣![]() (x+3),令x=0,得 y值,令y=0,得x值,可得点C、D的坐标,由此可得点H坐标,同理可得点G坐标,
(x+3),令x=0,得 y值,令y=0,得x值,可得点C、D的坐标,由此可得点H坐标,同理可得点G坐标,
由勾股定理得:m值,即可求得点A、B、C的坐标,从而得到 “母线”函数的表达式.
(1)由题意得:k=﹣3,b=6,
则答案为:y=![]() (x+6);
(x+6);
(2)令x=0,则y=4,令y=0,则x=2或﹣4,
点A、B、C的坐标分别为(2,0)、(0,4)、(﹣4,0),
则直线CD的表达式为:y=![]() (x+4)=
(x+4)=![]() x+2;
x+2;
(3)设点P的横坐标为m,则点P(m,n),n=﹣![]() m2﹣m+4,
m2﹣m+4,
则直线OP的表达式为:y=![]() x,
x,
将直线OP和CD表达式联立得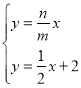 ,
,
解得:点Q(![]() ,
,![]() )
)
则![]() =﹣
=﹣![]() m2﹣
m2﹣![]() m+4,
m+4,
y=![]() =﹣
=﹣![]() m2﹣
m2﹣![]() m+3,
m+3,
当m=﹣![]() ,y最大值为
,y最大值为![]() ;
;
(4)直线CD的表达式为:y=﹣![]() (x+3),
(x+3),
令x=0,则y=﹣![]() ,令y=0,则x=﹣3,
,令y=0,则x=﹣3,
故点C、D的坐标为(﹣3,0)、(0,﹣![]() ),则点H(﹣
),则点H(﹣![]() ,﹣
,﹣![]() ),
),
同理可得:点G(﹣![]() ,
,![]() ),
),
则GH2=(![]() +
+![]() )2+(
)2+(![]() ﹣
﹣![]() )2=(
)2=(![]() )2,
)2,
解得:m=﹣3(正值已舍去),
则点A、B、C的坐标分别为(1,0)、(0,3)、(﹣3,0),
则“母线”函数的表达式为:y=a(x﹣1)(x+3)=a(x2﹣2x﹣3),
即:﹣3a=﹣3,解得:a=1,
故:“母线”函数的表达式为:y=x2﹣2x﹣3.