题目内容
【题目】某手机店销售一部A型手机比销售一部B型手机获得的利润多50元,销售相同数量的A型手机和B型手机获得的利润分别为3000元和2000元.
(1)求每部A型手机和B型手机的销售利润分别为多少元?
(2)该商店计划一次购进两种型号的手机共110部,其中A型手机的进货量不超过B型手机的2倍.设购进B型手机n部,这110部手机的销售总利润为y元.
①求y关于n的函数关系式;
②该手机店购进A型、B型手机各多少部,才能使销售总利润最大?
(3)实际进货时,厂家对B型手机出厂价下调m(30<m<100)元,且限定商店最多购进B型手机80台.若商店保持两种手机的售价不变,请你根据以上信息及(2)中的条件,设计出使这110部手机销售总利润最大的进货方案.
【答案】(1)每部A型手机的销售利润为150元,每部B型手机的销售利润为100元;
(2)①y=﹣50n+16500 (n≥36 );②购进A型手机73部、B型手机37部时,才能使销售总利润最大;(3)见解析.
【解析】
(1)设每部A型手机的销售利润为x元,每部B型手机的销售利润为y元,根据题意列出方程组求解;(2)①设购进B型手机n部,则购进A型手机(110﹣n)部,根据销售总利润=A型手机的利润+B型手机的利润列出函数解析式即可;②利用不等式求出n的范围,根据一次函数的性质解答即可;(3)据题意得,y=150(110-n)+(100+m)n,即y=(m-50)n+16500,分三种情况讨论,①当30<m<50时,y随n的增大而减小,②m=50时,m-50=0,y=16500,③当50<m<100时,m-50>0,y随n的增大而增大,分别进行求解即可解答.
(1)设每部A型手机的销售利润为x元,每部B型手机的销售利润为y元,
根据题意,得:![]() ,
,
解得:![]() ,
,
答:每部A型手机的销售利润为150元,每部B型手机的销售利润为100元;
(2)①设购进B型手机n部,则购进A型手机(110﹣n)部,
则y=150(110﹣n)+100n=﹣50n+16500,
其中,110﹣n≤2n,即n≥36![]() ,
,
∴y关于n的函数关系式为y=﹣50n+16500 (n≥36![]() );
);
②∵﹣50<0,
∴y随n的增大而减小,
∵n≥36![]() ,且n为整数,
,且n为整数,
∴当n=37时,y取得最大值,最大值为﹣50×37+16500=14650(元),
答:购进A型手机73部、B型手机37部时,才能使销售总利润最大;
(3)根据题意,得:y=150(110﹣n)+(100+m)n=(m﹣50)n+16500,
其中,36![]() ≤n≤80(n为整数),
≤n≤80(n为整数),
①当30<m<50时,y随n的增大而减小,
∴当n=37时,y取得最大值,
即购进A型手机73部、B型手机37部时销售总利润最大;
②当m=50时,m﹣50=0,y=16500,
即商店购进B型电脑数量满足36![]() ≤n≤80的整数时,均获得最大利润;
≤n≤80的整数时,均获得最大利润;
③当50<m<100时,y随n的增大而增大,
∴当n=80时,y取得最大值,
即购进A型手机30部、B型手机80部时销售总利润最大.

 期末100分闯关海淀考王系列答案
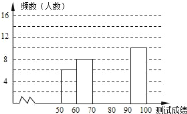
期末100分闯关海淀考王系列答案【题目】“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
(1)①频数分布表中a的值为;②若测试成绩不低于80分为优秀,则本次测试的优秀率是;③将频数分布直方图补充完整;
(2)第5组10名同学中,有4名男同学(用A,B,C,D表示),现将这4名同学分成两组(每组2人)进行对抗练习,求A与B两名男同学能分在同一组的概率.
组别 | 成绩x分 | 频数(人数) |
第1组 | 50≤x<60 | 6 |
第2组 | 60≤x<70 | 8 |
第3组 | 70≤x<80 | 14 |
第4组 | 80≤x<90 | a |
第5组 | 90≤x<100 | 10 |