题目内容
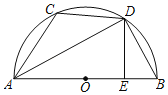
【题目】如图,四边形ABDC内接于半圆O,AB为直径,AD平分∠CAB,AB﹣AC=4,AD=3![]() ,作DE⊥AB于点E,则BE的长为_____,AC的长为_____.
,作DE⊥AB于点E,则BE的长为_____,AC的长为_____.
【答案】2, 5.
【解析】
作DF⊥AC交AC的延长线于F,证明Rt△DFC≌Rt△DEB(HL),推出CF=BE,证明Rt△ADF≌Rt△ADE(HL),推出AF=AE,由AB-AC=AE+EB-(AF-CF)=2BE=4,推出BE=2,由△ADE∽△ABD,推出![]() ,可得AD2=AEAB,设AE=x,由此建立方程即可解决.
,可得AD2=AEAB,设AE=x,由此建立方程即可解决.
如图,作DF⊥AC交AC的延长线于F.

∵AD平分∠CAB,DF⊥AC,DE⊥AB,
∴DE=DF,∠DAC=∠DAB
∴![]() ,
,
∴CD=DB,
∵∠F=∠DEB=90°,
∴Rt△DFC≌Rt△DEB(HL),
∴CF=BE,
∵∠F=∠AED=90°,AD=AD.DF=DE,
∴Rt△ADF≌Rt△ADE(HL),
∴AF=AE,
∵AB﹣AC=AE+EB﹣(AF﹣CF)=2BE=4,
∴BE=2,
∵AB是直径,
∴∠ADB=90°,
∵∠DAE=∠BAD,∠AED=∠ADB=90°,
∴△ADE∽△ABD,
∴![]() ,
,
∴AD2=AEAB,设AE=x,
则有:63=x(x+2),
解得x=7或﹣9(舍弃),
∴AE=7,
∴AB=AE+BE=9,
∵AB﹣AC=4,
∴AC=5,
故答案为:2,5.

练习册系列答案
相关题目