题目内容
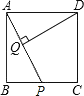
【题目】如图,在正方形ABCD中,AB=2,P是BC边上与B、C不重合的任意一点,DQ⊥AP于点Q
(1)判断△DAQ与△APB是否相似,并说明理由.
(2)当点P在BC上移动时,线段DQ也随之变化,设PA=x,DQ=y,求y与x间的函数关系式,并求出x的取值范围.
【答案】(1)△DAQ∽△APB,见解析;(2)y=![]() ,2<x<2
,2<x<2![]()
【解析】
(1)根据四边形ABCD是正方形,得AD∥BC,∠B=90°,∠DAP=∠APB,根据DQ⊥AP,得∠B=∠AQD,即可证出△DAQ∽△APB;
(2)根据△DAQ∽△APB,得![]() ,再把AB=2,DA=2,PA=x,DQ=y代入得出
,再把AB=2,DA=2,PA=x,DQ=y代入得出![]() ,y=
,y=![]() .根据点P在BC上移到C点时,PA最长,求出此时PA的长即可得出x的取值范围.
.根据点P在BC上移到C点时,PA最长,求出此时PA的长即可得出x的取值范围.
解:(1)∵四边形ABCD是正方形,
∴AD∥BC,∠B=90°,
∴∠DAP=∠APB,
∵DQ⊥AP,
∴∠AQD=90°,
∴∠B=∠AQD,
∴△DAQ∽△APB;
(2)∵△DAQ∽△APB,
∴![]() ,
,
∵AB=2,四边形ABCD是正方形,
∴DA=2,
∵PA=x,DQ=y,
∴![]() ,
,
∴y=![]() .
.
∵点P在BC上移到C点时,PA最长,此时PA=![]() ,
,
又∵P是BC边上与B、C不重合的任意一点,
∴x的取值范围是;2<x<2![]() .
.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
相关题目