题目内容
【题目】如图,已知反比例函数y=![]() 与一次函数y=x+b的图形在第一象限相交于点A(1,﹣k+4).
与一次函数y=x+b的图形在第一象限相交于点A(1,﹣k+4).
(1)试确定这两函数的表达式;
(2)求出这两个函数图象的另一个交点B的坐标,并求△AOB的面积;
(3)根据图象直接写出反比例函数值大于一次函数值的x的取值范围.

【答案】(1)![]() ,y=x+1;(2)
,y=x+1;(2)![]() ;(3)x<﹣2或0<x<1.
;(3)x<﹣2或0<x<1.
【解析】试题分析:(1)根据反比例函数y=![]() 与一次函数y=x+b的图形在第一象限相交于点A(1,﹣k+4),可以求得k的值,从而可以求得点A的坐标,从而可以求出一次函数y=x+b中b的值,本题得以解决;
与一次函数y=x+b的图形在第一象限相交于点A(1,﹣k+4),可以求得k的值,从而可以求得点A的坐标,从而可以求出一次函数y=x+b中b的值,本题得以解决;
(2)将第一问中求得的两个解析式联立方程组可以求得点B的坐标,进而可以求得△AOB的面积;
(3)根据函数图象可以解答本题.
试题解析:解:(1)∵反比例函数y=![]() 与一次函数y=x+b的图形在第一象限相交于点A(1,﹣k+4),∴
与一次函数y=x+b的图形在第一象限相交于点A(1,﹣k+4),∴![]() ,解得:k=2,∴点A(1,2),∴2=1+b,得:b=1,即这两个函数的表达式分别是:
,解得:k=2,∴点A(1,2),∴2=1+b,得:b=1,即这两个函数的表达式分别是: ![]() ,y=x+1;
,y=x+1;
(2)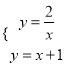
解得: ![]() 或
或![]() ,即这两个函数图象的另一个交点B的坐标是(﹣2,﹣1);
,即这两个函数图象的另一个交点B的坐标是(﹣2,﹣1);
将y=0代入y=x+1,得x=﹣1,∴OC=|﹣1|=1,∴S△AOB=S△AOC+S△BOC=![]() ,即△AOB的面积是
,即△AOB的面积是![]() ;
;
(3)根据图象可得反比例函数值大于一次函数值的x的取值范围是x<﹣2或0<x<1.

练习册系列答案
相关题目
【题目】已知关于m的方程![]() (m-16)=7的解也是关于x的方程2(x-3)-n=52的解.
(m-16)=7的解也是关于x的方程2(x-3)-n=52的解.
(1)求m,n的值;
(2)已知∠AOB=m°,在平面内画一条射线OP,恰好使得∠AOP=n∠BOP,求∠BOP.