题目内容
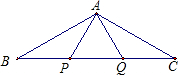 如图,已知P、Q是△ABC的边BC上的两点,且 BP=QC=PQ=AP=AQ,则∠BAC=
如图,已知P、Q是△ABC的边BC上的两点,且 BP=QC=PQ=AP=AQ,则∠BAC=分析:先根据BP=QC=PQ=AP=AQ求证△APQ为等边三角形,△ABP为等腰三角形,△AQC为等腰三角形,再根据三角形外角的性质求出∠QAC和∠BAP的度数即可.
解答:解:∵BP=QC=PQ=AP=AQ,
∴△APQ为等边三角形,△ABP为等腰三角形,△AQC为等腰三角形,
∴∠PAQ=∠APQ=∠AQP=60°,
在△ABP和△CAQ中
,
∴△ABP≌△ACQ,
∴∠QAC=∠B=
∠APQ=30°,
同理:∠BAP=30°,
∠BAC=∠BAP+∠PAQ+∠QAC=30°+60°+30°=120°.
故答案为:120°
∴△APQ为等边三角形,△ABP为等腰三角形,△AQC为等腰三角形,
∴∠PAQ=∠APQ=∠AQP=60°,
在△ABP和△CAQ中
|
∴△ABP≌△ACQ,
∴∠QAC=∠B=
| 1 |
| 2 |
同理:∠BAP=30°,
∠BAC=∠BAP+∠PAQ+∠QAC=30°+60°+30°=120°.
故答案为:120°
点评:此题主要考查学生对等腰三角形的判定与性质和三角形外角的性质的理解和掌握,此题的关键是判定出△APQ为等边三角形,△ABP为等腰三角形,△AQC为等腰三角形,然后利用外角的性质即可求解.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
 8、如图,已知△ABC的周长是34,其中AB=10,AO、BO分别是角平分线,且MN∥BA,分别交AC于N、BC于M,则△CMN的周长为( )
8、如图,已知△ABC的周长是34,其中AB=10,AO、BO分别是角平分线,且MN∥BA,分别交AC于N、BC于M,则△CMN的周长为( ) 如图,已知⊙O的半径是10,弦AB长为16.现要从弦AB和劣弧
如图,已知⊙O的半径是10,弦AB长为16.现要从弦AB和劣弧

 (2010•西藏)如图,已知E,F是四边形ABCD的对角线BD上两点,BF=DE,AF=CE,AF∥CE,
(2010•西藏)如图,已知E,F是四边形ABCD的对角线BD上两点,BF=DE,AF=CE,AF∥CE, 如图,已知△ABC,P是边AB上一点,连接CP,使△ACP∽△ABC成立的条件是( )
如图,已知△ABC,P是边AB上一点,连接CP,使△ACP∽△ABC成立的条件是( )