题目内容
8、如图，已知△ABC的周长是34，其中AB=10，AO、BO分别是角平分线，且MN∥BA，分别交AC于N、BC于M，则△CMN的周长为（ ）分析：由题意知，BC+AC=24，由角的平分线和平行线的性质证得△BMO和△AON为等腰三角形后，则△CMN的周长等于BC+AC．
解答：解：∵AO是角平分线，
∴∠BAO=∠NAO，
∵MN∥BA，
∴∠BAO=∠AON，
∴∠OAN=∠AON，
∴AN=ON，
同理：BM=OM，
∵△ABC的周长是34，AB=10，
∴BC+AC=24，
∴△CMN的周长=MC+MN+CN=MC+CN=ON+OM=BC+AC=24．
故选B．
∴∠BAO=∠NAO，
∵MN∥BA，
∴∠BAO=∠AON，
∴∠OAN=∠AON，
∴AN=ON，
同理：BM=OM，
∵△ABC的周长是34，AB=10，
∴BC+AC=24，
∴△CMN的周长=MC+MN+CN=MC+CN=ON+OM=BC+AC=24．
故选B．
点评：本题关键是要把△CMN的周长转化为BC+AC．
练习册系列答案
天天向上口算本系列答案
相关题目
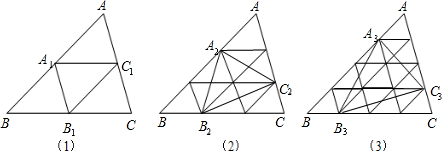
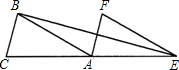如图，已知△ABC的面积为4，且AB=AC，现将△ABC沿CA方向平移CA的长度，得到△EFA．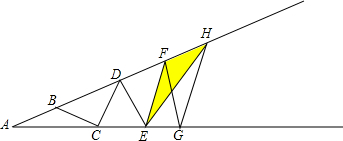
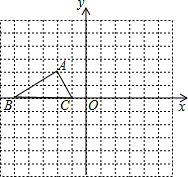（2010•孝感模拟）如图，已知△ABC的三个顶点的坐标分别为A（-2，2）、B（-5，0）、C（-1，0）．
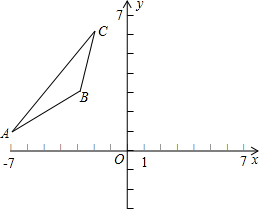如图，已知△ABC的三个顶点的坐标分别是A（-7，1），B（-3，3），C（-2，6）．