题目内容
【题目】(1)我们知道“三角形三个内角的和为 180°”.现在我们用平行线的性质来证明这个结论是正确的.
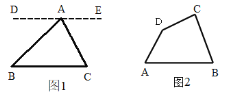
已知:∠BAC、∠B、∠C 是△ABC 的三个内角,如图 1.
求证:∠BAC+∠B+∠C=180° 证明:过点 A 作直线 DE∥BC(请你把证明过程补充完整)
(2)请你用(1)中的结论解答下面问题:
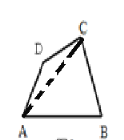
如图 2,已知四边形 ABCD,求∠A+∠B+∠C+∠D 的度数.
【答案】(1)详见解析 ;(2)360°
【解析】
(1)根据平行线性质和平角定义可得;(2)由(1)结论,连接AC.得到两个三角形△ABC和△ADC.
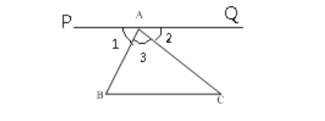
(1)证明:过点A作PQ∥BC
∴∠1=∠B(两直线平行,内错角相等)
∠2=∠C(两直线平行,内错角相等)
又∵∠1+∠2+∠3=180° (平角的定义)
∴∠BAC+∠B+∠C=180° (等量代换)
(2)连接AC.得到两个三角形△ABC和△ADC
∵三角形内角和是180°,所以两个就是360°.
∴∠A+∠B+∠C+∠D=360°

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目