Question

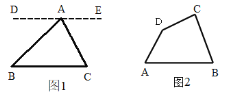
【题目】如图，在面积为3的△ABC中，AB=3，∠BAC=45°，点D是BC边上一点．

（1）若AD是BC边上的中线，求AD的长；

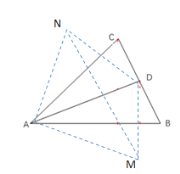
（2）点D关于直线AB和AC的对称点分别为点M、N，求AN的长度的最小值；

（3）若P是△ABC内的一点，求的最小值．

Answer 1

【答案】（1）见解析；（2）；（3）

【解析】

（1）作CE，DF分别垂直于AB于点E，F，已知CE⊥AB，S△ABC=3，∠BAC=45°，可得AE=CE=2，BE=1，因为DF∥CE，AD是BC边上的中线，可得BF=EF=，在Rt△AFD中利用勾股定理即可求出AD的长．

（2）在Rt△BEC中，求得BC，当AD⊥CB时，AN=AD最小，根据等面积法，即可求出AD．

（3）将△APB绕点A逆时针旋转90°得到△AFE，易知△AFP是等腰直角三角形，∠EAC=135°，作EH⊥BA交BA的延长线于H．在Rt△EAH中，可得EH=AH=2，在Rt△EHC中，求得EC，，的最小值即为CE的值．

（1）作CE，DF分别垂直于AB于点E，F

∵CE⊥AB，S△ABC=3，∠BAC=45°

∴，BE=1，

∵CE，DF分别垂直于AB于点E，F

∴DF∥CE

又∵AD是BC边上的中线

∴，

∴AF=

在Rt△AFD中，

∴

（2）在Rt△BEC中，BC=

当AD⊥CB时，AN=AD最小

根据等面积法，

得AN=

故答案为：

（3）将△APB绕点A逆时针旋转90°得到△AFE，易知△AFP是等腰直角三角形，∠EAC=135°，作EH⊥BA交BA的延长线于H．

在Rt△EAH中，

∵∠H=90°，∠EAH=45°，

∴EH=AH=2，

在Rt△EHC中，

∴的最小值为．