题目内容
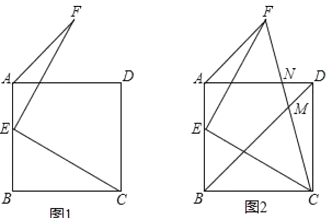
【题目】如图1,点![]() 为正方形
为正方形![]() 的边
的边![]() 上一点,
上一点,![]() ,且
,且![]() ,连接
,连接![]() .
.
(1)求![]() 的度数;
的度数;
(2)如图2,连接![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() .
.
求证:![]() .
.
【答案】(1)135°;(2)见详解.
【解析】
(1)过点F作FM⊥AB交AB的延长线于点M,证明△EBC△FME,即可解决问题;
(2)过点F作FG//AB交BD于点G.先证明四边形ABGF为平行四边形,再证明△FGM△CDM,即可解决问题.
(1)过点F作FM⊥AB交AB的延长线于点M,
∵四边形ABCD是正方形,
∴∠B=∠M=∠CEF=90°,
∴∠MEF+∠CEB=90°,∠CEB+∠BCE=90°,
∴∠MEF=∠ECB,
∵EC=EF,
∴△EBC△FME(AAS) ,
∴FM=BE,EM=BC,
∵BC=AB,
∴EM=AB,
∴EMAE=ABAE,
∴AM=BE,
∴FM=AM,
∵FM⊥AB,
∴∠MAF=45°,
∴∠EAF=135°;
(2)过点F作FG//AB交BD于点G.
由(1)可知∠EAF=135°,
∵∠ABD=45°,
∴∠EAF+∠ABD=180°,
∴AF//BG,
∵FG//AB,
∴四边形ABGF为平行四边形,
∴AF=BG,FG=AB,
∵AB=CD,
∴FG=CD,
∵AB//CD,
∴FG//CD,
∴∠FGM=∠CDM,
∵∠FMG=∠CMD
∴△FGM△CDM(AAS),
∴GM=DM,
∴DG=2DM,
∴BD=BG+DG=AF+2DM.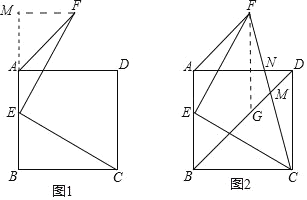

练习册系列答案
相关题目