题目内容
【题目】已知锐角三角形ABC内接于⊙O，AD⊥BC，垂足为D．
（1）如图1， 
，BD＝DC，求∠B的度数；
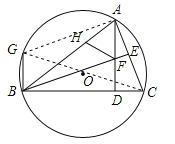
（2）如图2，BE⊥AC，垂足为E，BE交AD于点F，过点B作BG∥AD交⊙O于点G，在AB边上取一点H，使得AH＝BG．求证：△AFH是等腰三角形．
【答案】（1）∠B=60°；（2）证明见解析．
【解析】试题分析：（1）先根据弧AB=弧BC可知AB=BC，再由AD⊥BC，BD=DC可知AD是线段BC的垂直平分线，故AB=AC，由此可知△ABC是等边三角形，故可得出结论；
（2）连接GC，GA，根据BG⊥BC可知GC是⊙O的直径，故∠GAC=90°，由此可判断出四边形GBFA是平行四边形，由平行四边形的性质即可得出结论．
试题解析：解：（1）∵弧AB=弧BC，∴AB=BC．
∵AD⊥BC，BD=DC，∴AD是线段BC的垂直平分线，∴AB=AC，∴△ABC是等边三角形，∴∠B=60°；
（2）连接GC，GA，∵BG⊥BC，∴GC是⊙O的直径，∴∠GAC=90°．
∵BE⊥AC，∴∠BEC=∠GAC=90°，∴AG∥BE．
∵AD⊥BC，∴∠ADC=∠GBC=90°，∴BG∥AD，∴四边形GBFA是平行四边形，∴BG=AF．
∵BG=AH，∴AH=AF，∴△AFH是等腰三角形．
练习册系列答案
相关题目
