Question

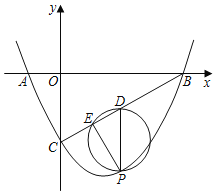
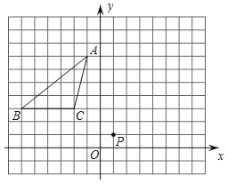
【题目】某校积极推行“互动生成的学本课堂”卓有成效，“小组合作学习”深入人心，九年级某学习小组在操作实践过程中发现了一个有趣的问题：将直尺和三角板（三角板足够大）按如图所示的方式摆放在平面直角坐标系中，直尺的左侧边CD在直线x＝4上，在保证直角三角板其中一条直角边始终过点A（0，4），同时使得直角顶点E在CD上滑动，三角板的另一直角边与x轴交于点B，当点E从点C（4，5）滑动到点D（4，0）的过程中，点B所经过的路径长为_____．

Answer 1

【答案】

【解析】

过点A作AF⊥CD于F，分点E在点F上方和点F下方两种情况讨论，通过相似三角形的性质和二次函数的性质可求解．

解：如图，过点A作AF⊥CD于F，则AF=4，CF=1，

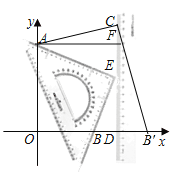
当点E与点C重合时，三角板与x轴交于点B'，

∵∠ACB'=90°，AF⊥CD，

∴∠ACF+∠B'CD=90°，∠CAF+∠ACF=90°，

∴∠CAF=∠B'CD，且∠AFC=∠B'DC=90°，

∴△ACF∽△CB'D，

∴，

∴，

∴B'D=，

∴点E从点C到点F，点B所经过的路径为，

当点E从点F到点D时，∵∠AEF+∠BED=90°，∠AEF+∠EAF=90°，

∴∠BED=∠EAF，

又∵∠AFE=∠EDB=90°，

∴△AEF∽△EBD，

∴，

∴

∴BD=，

∴当EF=2时，BD有最大值为1，

∴点E从点F到点D，点B所经过的路径为2，

∴点B所经过的路径长=2+=，

故答案为：．