题目内容
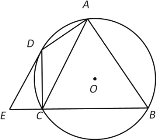
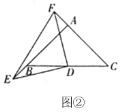
【题目】如图，将边长为8的正方形纸片ABCD沿着EF折叠，使点C落在AB边的中点M处．点D落在点D'处，MD'与AD交于点G，则△AMG的内切圆半径的长为______.
【答案】
【解析】
由勾股定理可求ME=5，BE=3，通过证明△AMG∽△BEM，可得AG=
，GM=
，即可求解．
∵将边长为8的正方形纸片ABCD沿着EF折叠，使点C落在AB边的中点M处．
∴ME=CE，MB=
AB=4=AM，∠D'ME=∠C=90°，
在Rt△MBE中，ME2=MB2+BE2，
∴ME2=16+（8-ME）2，
∴ME=5，
∴BE=3，
∵∠D'ME=∠DAB=90°=∠B
∴∠EMB+∠BEM=90°，∠EMB+∠AMD'=90°
∴∠AMD'=∠BEM，且∠GAM=∠B=90°
∴△AMG∽△BEM
∴
∴
，
∴AG=，GM=
∴△AMG的内切圆半径的长=
故答案为：.
【题目】小明同学以“你最喜欢的运动项目”为主题，对公园里参加运动的群众进行随机调查（每名被调查者只能选一个项目，且被调查者都进行了选择）.下面是小明根据调查结果列出的统计表和绘制的扇形统计图（不完整）.
被调查者男、女所选项目人数统计表
项目 | 男（人数） | 女（人数） |
广场舞 | 7 | 9 |
健步走 |
| 4 |
器械 | 2 | 2 |
跑步 | 5 |
|
根据以上信息回答下列问题：
（1）统计表中的
__________，
__________.
（2）扇形统计图中“广场舞”项目所对应扇形的圆心角度数为__________°.
（3）若平均每天来该公园运动的人数有3600人，请你估计这3600人中最喜欢的运动项目是“跑步”的约有多少人？
【题目】如图，点P是以O为圆心，AB为直径的半圆上的动点，AB=6cm，设弦AP的长为xcm，△APO的面积为ycm2，（当点P与点A或点B重合时，y的值为0）．小明根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究．下面是小明的探究过程，请补充完整；
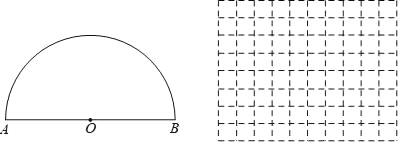
（1）通过取点、画图、测量、计算，得到了x与y的几组值，如下表：
x/cm | 0.5 | 1 | 2 | 3 | 3.5 | 4 | 5 | 5.5 | 5.8 |
y/cm2 | 0.8 | 1.5 | 2.8 | 3.9 | 4.2 | m | 4.2 | 3.3 | 2.3 |
那么m= ；（保留一位小数）
（2）建立平面直角坐标系，描出以表中各组对应值为坐标的点，画出该函数图象．
（3）结合函数图象说明，当△APO的面积是4时，则AP的值约为 ．（保留一位小数）
