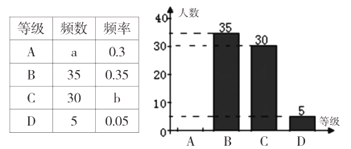
题目内容
【题目】如图，在ABCD中，∠DAB＝60°，AB＝8，AD＝6．⊙O分别切边AB，AD于点E，F，且圆心O好落在DE上．现将⊙O沿AB方向滚动到与BC边相切（点O在ABCD的内部），则圆心O移动的路径长为（ ）
A.2B.4C.5﹣
D.8﹣2
【答案】B
【解析】
如图所示，⊙O滚过的路程即线段EN的长度. EN=AB-AE-BN，所以只需求AE、BN的长度即可.分别根据AE和BN所在的直角三角形利用三角函数进行计算即可.
解：连接OE，OA、BO．
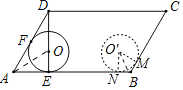
∵AB，AD分别与⊙O相切于点E、F，
∴OE⊥AB，OF⊥AD，
∴∠OAE＝∠OAD＝30°，
在Rt△ADE中，AD＝6，∠ADE＝30°，
∴AE＝
AD＝3，
∴OE＝
AE＝
，
∵AD∥BC，∠DAB＝60°，
∴∠ABC＝120°．
设当运动停止时，⊙O′与BC，AB分别相切于点M，N，连接O′N，O′M．
同理可得，∠BO′N为30°，且O′N为，
∴BN＝O′Ntan30°＝1cm，
EN＝AB﹣AE﹣BN＝8﹣3﹣1＝4．
∴⊙O滚过的路程为4．
故选：B．
练习册系列答案
阅读快车系列答案
相关题目
