题目内容
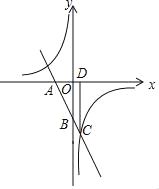
【题目】如图,在平面直角坐标系xOy中,直线AB与x轴、y轴分别交于点A、B,与反比例函数y=![]() 的图象在第四象限交于点C,CD⊥x轴于点D,tan∠OAB=2,OA=2,OD=1.
的图象在第四象限交于点C,CD⊥x轴于点D,tan∠OAB=2,OA=2,OD=1.
(1)求该反比例函数的表达式;
(2)点M是这个反比例函数图象上的点,过点M作MN⊥y轴,垂足为点N,连接OM、AN,如果S△ABN=2S△OMN,直接写出点M的坐标.
【答案】(1)y=![]() ;(2)点M的坐标为(﹣3,2)或(
;(2)点M的坐标为(﹣3,2)或(![]() ,﹣10).
,﹣10).
【解析】
(1)由OA=2、OD=1知AD=3,根据tan∠OAB=2求得CD=6,据此可得答案;
(2)设点M(a,﹣![]() ),可得S△OMN=3、S△ABN=
),可得S△OMN=3、S△ABN=![]() ×OA×BN|=|4﹣
×OA×BN|=|4﹣![]() |,根据S△ABN=2S△OMN建立方程,解之求得a的值即可得.
|,根据S△ABN=2S△OMN建立方程,解之求得a的值即可得.
解:(1)∵AO=2,OD=1,
∴AD=AO+OD=3,
∵CD⊥x轴于点D,
∴∠ADC=90°.
在Rt△ADC中,CD=ADtan∠OAB=6.
∴C(1,﹣6),
∴该反比例函数的表达式是y=![]() .
.
(2)如图所示,
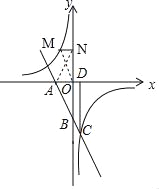
设点M(a,﹣![]() ),
),
∵MN⊥y轴,
∴S△OMN=![]() ×|﹣6|=3,S△ABN=
×|﹣6|=3,S△ABN=![]() ×OA×BN=
×OA×BN=![]() ×2×|4﹣
×2×|4﹣![]() |=|4﹣
|=|4﹣![]() |,
|,
∵S△ABN=2S△OMN,
∴|4﹣![]() |=6,
|=6,
解得:a=﹣3或a=![]() ,
,
当a=﹣3时,﹣![]() =2,即M(﹣3,2),
=2,即M(﹣3,2),
当a=![]() 时,﹣
时,﹣![]() =﹣10,即M(
=﹣10,即M(![]() ,﹣10),
,﹣10),
故点M的坐标为(﹣3,2)或(![]() ,﹣10).
,﹣10).

 阅读快车系列答案
阅读快车系列答案【题目】阅读对人成长的影响是巨大的,一本好书往往能改变人的一生,1995年联合国教科文组织把每年4月23日确定为“世界读书日”.如图是某校三个年级学生人数分布扇形统计图,其中八年级人数为400人,如表是该校学生阅读课外书籍情况统计表.请你根据图表中的信息,解答下列问题:
图书种类 | 频数 | 频率 |
科普常识 | 1600本 | B |
名人传记 | 1280本 | 0.32 |
漫画丛书 | A本 | 0.24 |
其它 | 160本 | 0.04 |
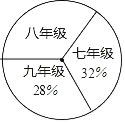
(1)求该校八年级的人数占全校总人数的百分率为 ;
(2)表中A= ,B= ;
(3)该校学生平均每人读多少本课外书?