题目内容
【题目】已知,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点.
的中点.
(1)若点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,则线段
的中点,则线段![]() 与
与![]() 的数量关系是 ;线段
的数量关系是 ;线段![]() 与
与![]() 的位置关系是 ;
的位置关系是 ;
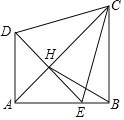
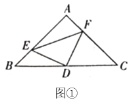
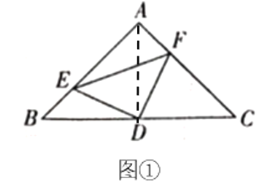
(2)如图①,若点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的点,且
上的点,且![]() ,上述结论是否依然成立,若成立,请证明;若不成立,请说明理由;
,上述结论是否依然成立,若成立,请证明;若不成立,请说明理由;
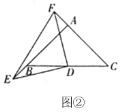
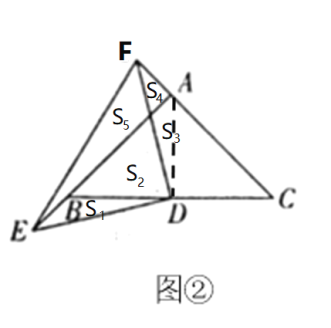
(3)如图②,若点![]() 、
、![]() 分别为
分别为![]() 、
、![]() 延长线上的点,且
延长线上的点,且![]() ,直接写出
,直接写出![]() 的面积.
的面积.
【答案】(1)![]() ,
,![]() ;(2)成立,证明见解析;(3)17.
;(2)成立,证明见解析;(3)17.
【解析】
(1)点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,及
的中点,及![]() ,可得:
,可得:![]() ,根据SAS判定
,根据SAS判定![]()
![]() ,即可得出
,即可得出![]() ,
,![]() ,可得
,可得![]() ,即可证
,即可证![]() ;
;
(2)根据SAS判定![]() ,即可得出
,即可得出![]() ,
,![]() ,可得
,可得![]() ,即可证
,即可证![]() ;
;
(3)根据SAS判定![]() ,即可得出
,即可得出![]() ,将
,将![]() 转化为:
转化为:![]() 进行求解即可.
进行求解即可.
解:(1)证明:连接![]() ,
,
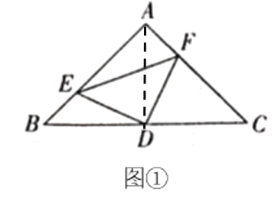
∵点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,
的中点,
∴![]()
∵![]() ,
,
∴![]()
∵![]() ,
,![]() ,
,![]() 为
为![]() 中点,
中点,
∴![]() ,且
,且![]() 平分
平分![]() ,
,![]() .
.
∴![]()
在![]() 和
和![]() 中,
中,
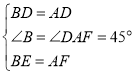 ,
,
∴![]() ,
,
∴![]() ,
,![]()
∵![]() ,
,
∴![]() ,
,
即![]() ,即
,即![]()
故答案为:![]() ,
,![]() ;
;
(2)结论成立:![]() ,
,![]() ;
;
证明:连接![]() ,
,
∵![]() ,
,![]() ,
,![]() 为
为![]() 中点,
中点,
∴![]() ,且
,且![]() 平分
平分![]() ,
,![]() .
.
∴![]()
在![]() 和
和![]() 中,
中,
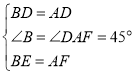 ,
,
∴![]() ,
,
∴![]() ,
,![]()
∵![]() ,
,
∴![]() ,
,
即![]() ,即
,即![]()
(3)证明:连接![]() ,
,
∵![]()
∴![]()
∴![]()
∵![]() ,
,![]() ,
,![]() 为
为![]() 中点,
中点,
∴![]() ,且
,且![]() 平分
平分![]() ,
,![]() ,
,![]()
![]()
∴![]()
∴![]()
∴![]()
在![]() 和
和![]() 中,
中,
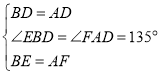 ,
,
∴![]() ,
,
∴![]()
即![]()
∵![]() 为
为![]() 中点,
中点,
∴![]()
∵![]() ,
,
∴![]() ,
,
∴![]()
故答案为:17

【题目】某校为了解七年级学生的体重情况,随机抽取了七年级m名学生进行调查,将抽取学生的体重情况绘制如下不完整的频数分布表和扇形统计图.
组别 | 体重(千克) | 人数 |
A | 37.5≤x<42.5 | 10 |
B | 42.5≤x<47.5 | n |
C | 47.5≤x<52.5 | 40 |
D | 52.5≤x<57.5 | 20 |
E | 57.5≤x<62.5 | 10 |

请根据图表信息回答下列问题:
(1)填空:①m=_____,②n=_____,③在扇形统计图中,C组所在扇形的圆心角的度数等于_______度;
(2)若把每组中各个体重值用这组数据的中间值代替(例如:A组数据中间值为40千克),则被调查学生的平均体重是多少千克?
(3)如果该校七年级有1000名学生,请估算七年级体重低于47.5千克的学生大约有多少人?