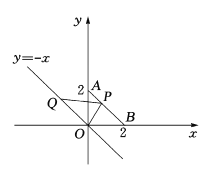
题目内容
【题目】如图,在平面直角坐标系中,点![]() 的坐标是
的坐标是![]() ,点
,点![]() 的坐标是
的坐标是![]() ,连结
,连结![]() ,点
,点![]() 是线段
是线段![]() 上的一个动点(包括两端点),直线
上的一个动点(包括两端点),直线![]() 上有一动点
上有一动点![]() ,连结
,连结![]() ,已知
,已知![]() 的面积为
的面积为![]() ,则点
,则点![]() 的坐标为__________________.
的坐标为__________________.
【答案】![]() 或
或![]()
【解析】
由A、B点的坐标可得出直线AB的解析式,从而发现直线AB与直线OQ平行,由平行线间距离处处相等,可先求出点O到直线AB的距离,结合三角形面积公式求出线段OQ的长度,再依据两点间的距离公式可得出结论.
∵点Q在直线y=x上,
∴设点Q的坐标为(m,m).
∵点A的坐标是(0,2),点B的坐标是(2,0),
∴△AOB为等腰直角三角形,
点O(0,0)到AB的距离h=![]() OA=2.
OA=2.
设直线AB的解析式为y=kx+b,
∵点A(0,2),点B(2,0)在直线AB上,
∴有![]() ,解得
,解得![]() .
.
即直线AB的解析式为y=x+2,
∵直线y=x+2与y=x平行,
∴点P到底OQ的距离为![]() (平行线间距离处处相等).
(平行线间距离处处相等).
∵△OPQ的面积S△OPQ=![]() OQh=
OQh=![]() OQ=
OQ=![]() ,
,
∴OQ=2.
由两点间的距离公式可知OQ=![]() =2,
=2,
解得:m=±![]() ,
,
∴点Q的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
故答案为:(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目