Question

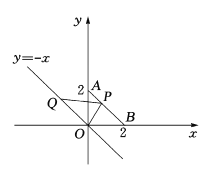
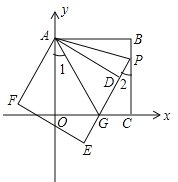
【题目】边长相等的两个正方形ABCO、ADEF如图摆放，正方形ABCO的边OA、OC在坐标轴上，ED交线段OC于点G，ED的延长线交线段BC于点P，连AG，已知OA长为.

（1）求证：;

（2）若，AG=2，求点G的坐标；

（3）在（2）条件下，在直线PE上找点M，使以M、A、G为顶点的三角形是等腰三角形，求出点M的坐标.

Answer 1

【答案】（1）证明见解析；（2）；（3）M坐标为或（．

【解析】

（1）由AO＝AD，AG＝AG，根据斜边和一条直角边对应相等的两个直角三角形全等，判断出即可；

（2）在中，由，，根据勾股定理求出OG的长，即可求出点G坐标；

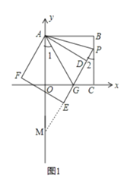
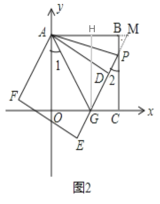
（3）根据题意，分两种情况：①如图1，当点M在 y轴的负半轴上时；②如图2，当点M在GP延长线上时，作GH⊥AB于点H，通过全等三角形的性质及等边三角形的性质可得出点M为所求的点，再结合点A、点G的坐标即可求出点M的坐标．

（1）证明：在Rt△AOG和Rt△ADG中，

∴△AOG≌△ADG（HL）．

（2）解：∵在中，，，

∴,

∴G点坐标为．

（3）①如图1，延长GE交轴于点M，
∵△AOG≌△ADG，
∴，

又∵，，

∴，

∵，

∴,

在△AOG和△MOG中，

∴，

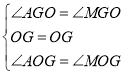
∴AG＝MG，

∴△AGM为等腰三角形，

∵点A坐标为，
∴点M坐标为．

②如图2，延长GP与AB的延长线交于点M，作GH⊥AB于点H．

∵，
∴，
∴；

∴，

∴为等边三角形，

∴GH垂直平分线AM．

∵，，

∴，

∴点M坐标为．
综上可得点M坐标为或．