Question

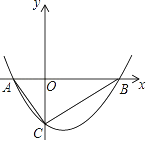
【题目】在平面直角坐标系中，O为原点，点A（3，0），点B（0，4），把△ABO绕点A顺时针旋转，得△AB′O′，点B，O旋转后的对应点为B′，O．

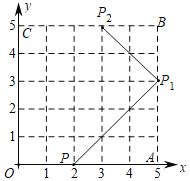
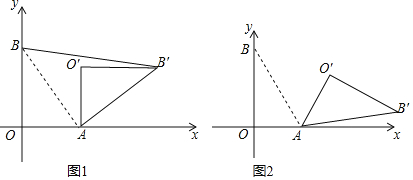
（1）如图1，当旋转角为90°时，求BB′的长；

（2）如图2，当旋转角为120°时，求点O′的坐标；

（3）在（2）的条件下，边OB上的一点P旋转后的对应点为P′，当O′P+AP′取得最小值时，求点P′的坐标．（直接写出结果即可）

Answer 1

【答案】（1）5；（2）O'（，）；（3）P'（，）.

【解析】

（1）先求出AB．利用旋转判断出△ABB'是等腰直角三角形，即可得出结论；

（2）先判断出∠HAO'=60°，利用含30度角的直角三角形的性质求出AH，OH，即可得出结论；

（3）先确定出直线O'C的解析式，进而确定出点P的坐标，再利用含30度角的直角三角形的性质即可得出结论．

（1）∵A（3，0），B（0，4），∴OA=3，OB=4，∴AB=5，由旋转知，BA=B'A，∠BAB'=90°，∴△ABB'是等腰直角三角形，∴BB'=AB=5；

（2）如图2，过点O'作O'H⊥x轴于H，由旋转知，O'A=OA=3，∠OAO'=120°，∴∠HAO'=60°，∴∠HO'A=30°，∴AH=AO'=，OH=AH=，∴OH=OA+AH=，∴O'（）；

（3）由旋转知，AP=AP'，∴O'P+AP'=O'P+AP．如图3，作A关于y轴的对称点C，连接O'C交y轴于P，∴O'P+AP=O'P+CP=O'C，此时，O'P+AP的值最小．

∵点C与点A关于y轴对称，∴C（﹣3，0）．

∵O'（），∴直线O'C的解析式为y=x+，令x=0，∴y=，∴P（0，），∴O'P'=OP=，作P'D⊥O'H于D．

∵∠B'O'A=∠BOA=90°，∠AO'H=30°，∴∠DP'O'=30°，∴O'D=O'P'=，P'D=O'D=，∴DH=O'H﹣O'D=，O'H+P'D=，∴P'（）．