题目内容
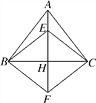
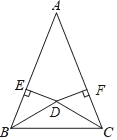
【题目】如图,点D是△ABC内部的一点,BD=CD,过点D作DE⊥AB,DF⊥AC,垂足分别为E、F,且BE=CF.求证:AB=AC.
【答案】证明见解析.
【解析】
欲证明AB=AC,只要证明∠ABC=∠ACB即可,根据“HL”证明Rt△BDE≌Rt△CDF,由全等三角形的性质可证∠EBD=∠FCD,再由等腰三角形的性质∠DBC=∠DCB,从而可证∠ABC=∠ACB.
∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°.
在Rt△BDE和Rt△CDF中,
![]()
∴Rt△BDE≌Rt△CDF(HL),
∴∠EBD=∠FCD,
∵BD=CD,
∴∠DBC=∠DCB,
∴∠DBC+∠EBD=∠DCB+∠FCD,
即∠ABC=∠ACB,
∴AB=AC.

练习册系列答案
相关题目