题目内容
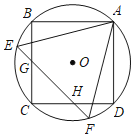
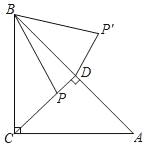
【题目】如图,在△ABC中,∠ACB=90°,AC=BC=4,P是△ABC的高CD上一个动点,以B点为旋转中心把线段BP逆时针旋转45°得到BP′,连接DP′,则DP′的最小值是( )
A.2![]() -2B.4﹣2
-2B.4﹣2![]() C.2﹣
C.2﹣![]() D.
D.![]() -1
-1
【答案】A
【解析】
在BC上截取BE=BD,根据等腰直角三角形的性质求得BA和BE,再由旋转的性质证明△BDP'≌△BEP,从而可得到PE=P'D,再由等腰直角三角形的性质求得PE,从而求得DP′的最小值.
解:如图,在BC上截取BE=BD,

∵∠ACB=90°,AC=BC=4, CD⊥AB,
∴BA=4![]() ,∠ABC=∠BAC=∠BCD=∠DCA=45°,BD=CD=AD=2
,∠ABC=∠BAC=∠BCD=∠DCA=45°,BD=CD=AD=2![]() =BE,
=BE,
∵旋转
∴BP=BP',∠PBP'=45°,
∵BE=BD,∠ABC=∠PBP'=45°,BP=BP'
∴△BDP'≌△BEP(SAS)
∴PE=P'D
∴当PE⊥CD时,PE有最小值,即DP'有最小值,
∵PE⊥CD,∠BCD=45°,
∴CE=![]() PE=BC﹣BE=4﹣2
PE=BC﹣BE=4﹣2![]()
∴P'D =PE=2![]() ﹣2
﹣2
故选:A.

【题目】甲、乙两个批发店销售同一种苹果,在甲批发店,不论一次购买数量是多少,价格均为5元/![]() .在乙批发店,一次购买数量不超过
.在乙批发店,一次购买数量不超过![]() 时,价格为7元/
时,价格为7元/![]() ;一次购买数量超过
;一次购买数量超过![]() 时,其中有
时,其中有![]() 的价格为6元/
的价格为6元/![]() ,超过
,超过![]() 部分的价格为4元/
部分的价格为4元/![]() .设小张在同一个批发店一次购买苹果的数量为
.设小张在同一个批发店一次购买苹果的数量为![]() .
.
(1)根据题意填表:
一次购买数量/ | 20 | 50 | 150 | … |
甲批发店花费/元 | 250 | … | ||
乙批发店花费/元 | 350 | … |
(2)设在甲批发店花费![]() 元,在乙批发店花费
元,在乙批发店花费![]() 元,分别求
元,分别求![]() ,
,![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)根据题意填空:
①若小张在甲批发店和在乙批发店一次购买苹果的数量相同,且花费相同,则他在同一个批发店一次购买苹果的数量为_________![]() ;
;
②若小张在同一个批发店一次购买苹果的数量为![]() ,则他在甲、乙两个批发店中的___________批发店购买花费少;
,则他在甲、乙两个批发店中的___________批发店购买花费少;
③若小张在同一个批发店一次购买苹果花费了460元,则他在甲、乙两个批发店中的___________批发店购买数量多.