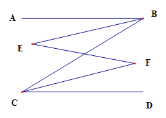
题目内容
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、
、![]() 同时从点
同时从点![]() 出发,以相同的速度分别沿折线
出发,以相同的速度分别沿折线![]() 、射线
、射线![]() 运动,连接
运动,连接![]() .当点
.当点![]() 到达点
到达点![]() 时,点
时,点![]() 、
、![]() 同时停止运动.设
同时停止运动.设![]() ,
,![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() .
.
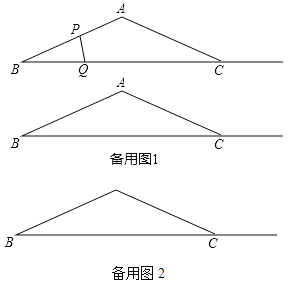
(1)求![]() 长;
长;
(2)求![]() 关于
关于![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;
的取值范围;
(3)请直接写出![]() 为等腰三角形时
为等腰三角形时![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2) ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)过点A作AM⊥BC于点M,由等腰三角形的性质可得∠B=∠C=30°,BM=CM=![]() BC,由直角三角形的性质可得BM=2
BC,由直角三角形的性质可得BM=2![]() ,即可求BC的值;
,即可求BC的值;
(2)分点P在AB上,点P在AC上,点Q在BC的延长线上时,三种情况讨论,由三角形的面积公式可求S关于x的函数关系式;
(3)分两种情况讨论,由等腰三角形的性质可求解.
解:(1)过点![]() 作
作![]() 于点
于点![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() .
.
∴![]() .
.
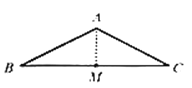
(2)因为点![]() ,
,![]() 同时出发且速度相同,所以两点运动的路程相同
同时出发且速度相同,所以两点运动的路程相同
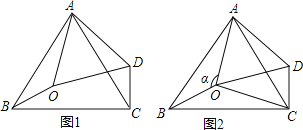
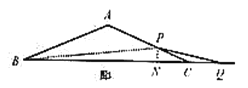
情况①:当![]() 时,此时点
时,此时点![]() 在线段
在线段![]() 上,如图1
上,如图1
过点![]() 作
作![]() 于点
于点![]() ,
,
在![]() 中,
中,
∵![]() ,
,![]() ,
,
∴![]() .
.
∴![]() 与
与![]() 重叠部分的面积
重叠部分的面积![]() .
.
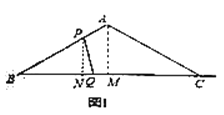
情况②:当![]() 时,此时点
时,此时点![]() 在线段
在线段![]() 上,如图2
上,如图2
过点![]() 作
作![]() 于点
于点![]() ,
,
此时,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
在![]() 中,
中,
∵![]() ,
,![]() ,
,
∴![]() .
.
∴![]() 与
与![]() 重叠部分的面积
重叠部分的面积![]() .
.
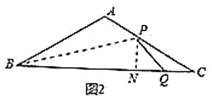
情况③:当![]() 时,此时点
时,此时点![]() 在线段
在线段![]() 上,
上,![]() 在线段
在线段![]() 延长线上,如图3
延长线上,如图3
过点![]() 作
作![]() 于点
于点![]() ,
,
由情况②同理可得:![]() ,
,
∴![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() 的面积,
的面积,
则![]()
![]() .
.
综上所述:![]() 与
与![]() 重叠部分的面积
重叠部分的面积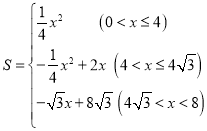 .
.
(3)![]() 或
或![]()
①当点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上时,
上时,![]() 不可能是等腰三角形.
不可能是等腰三角形.
②当点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上时,
上时,![]() ,
,![]() ,
,
③当点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 的延长线时,
的延长线时,![]() ,
,![]() .
.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目