题目内容
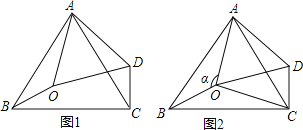
【题目】如图1，在△ABC中，∠BAC=60°，点0是△ABC内一点，△AB0
△ACD，连接OD.
（1）求证△AOD为等边三角形。
（2）如图2，连接OC，若∠BOC=130°，∠AOB=
.
①求∠OCD的度数
②当△OCD是等腰三角形时，求∠的度数
、
【答案】（1）见解析;.（2）①∠OCD=70°；②可以是130°，100°，115°.
【解析】
（1）根据全等三角形得到AO=AD，∠BAO=∠CAD，由∠BAC=60°，求得∠OAD=60°，即可得到结论；
（2）①根据△AOD为等边三角形，求得∠AOD=∠ADO=60°，求得∠DOC=360°-α-130°-60°=170°-α，根据全等三角形的性质得到∠ADC=∠AOB=α，于是得到∠OCD=180°-∠DOC-∠ODC=70°；②当△OCD是等腰三角形时，（Ⅰ）当OD=OC，由∠DOC=170°-α，得到∠OCD=∠ODC= 
α+5°，列方程得到α=130°（Ⅱ）当OD=CD，于是得到∠OCD=∠COD=170°-α；求得∠ODC=180°-2×170°+2α=2α-160°，列方程即可得到α=100°；（Ⅲ）当OC=CD，于是得到∠ODC=∠COD=170°-α，列方程即可得到α=115°．
（1）证明：∵△ABO≌△ACD
∴∠OAB=∠CAD
∴AO=AD
∴∠OAB+∠OAC=∠OAC+∠CAD=60°
△AOD为等边三角形.
(2)①∵△AOD为等边三角形，
∴∠AOD=∠ADO=60°，
∵∠BOC=130°，∠AOB=∠α，
∴∠DOC=360°α130°60°=170°α，
∵△ABO≌△ACD，
∴∠ADC=∠AOB=α，
∴∠ODC=α60°，
∴∠OCD=180°∠DOC∠ODC=70°；
②当△OCD是等腰三角形时，
(Ⅰ)当OD=OC,∵∠DOC=170°α，
∴∠OCD=∠ODC=α+5°，
∴60°+
α+5°=α，
解得：α=130°
(Ⅱ)当OD=CD,∴∠OCD=∠COD=170°α；
∴∠ODC=180°2×170°+2α=2α160°，
∴60°+2α160°=α，
解得：α=100°；
(Ⅲ)当OC=CD,∴∠ODC=∠COD=170°α，
∴170°α+60°=α，
解得：α=115°.
综上所述：当△OCD是等腰三角形时,∠α的度数为：130°,100°,115°.
