题目内容
【题目】如图,正方形ABCD中,点E、F分别在边BC和DC上,连接AE、BF,AE⊥BF,点M、N分别在边AB、DC上,连接MN,若MN∥BC,FN=1,BE=2,则BM=_____.
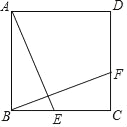
【答案】1或3
【解析】
根据正方形的性质,可得∠ABC与∠C的关系,AB与BC的关系,根据两直线垂直,可得∠AOB的度数,根据同角的余角相等可得∠BAO=∠CBF,根据ASA,可得△ABE≌△BCF,得BE=CF=2,分情况讨论,证明四边形MBCN是平行四边形,则BM=CN,根据两图形可得BM的长.
解:∵四边形ABCD是正方形,
∴∠ABC=∠C=90°,AB=BC.
∵AE⊥BF,
∴∠AOB=∠BAO+∠ABO=90°,
∵∠ABO+∠CBF=90°,
∴∠BAO=∠CBF.
在△ABE和△BCF中,
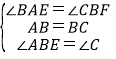 ,
,
∴△ABE≌△BCF(ASA),
∴BE=CF=2,
∵MN∥BC,AB∥CD,
∴四边形MBCN是平行四边形,
∴BM=CN,
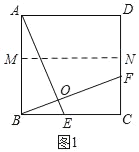
①当N在F的上方时,如图1,
∴BM=CN=CF+FN=2+1=3,
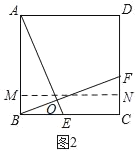
②当N在F的下方时,如图2,
∴BM=CN=CF﹣FN=2﹣1=1,
∴BM的长为1或3,
故答案为:1或3

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目