题目内容
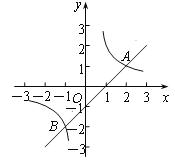
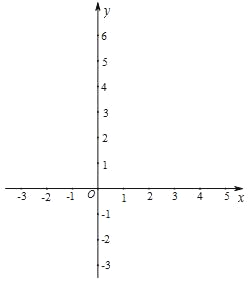
【题目】在平面直角坐标系xOy中,直线y=kx+b(k≠0)与x轴交于点A,与y轴交于点B,与反比例函数y=![]() (m≠0)的图象在第一象限交于点P(1,3),连接OP.
(m≠0)的图象在第一象限交于点P(1,3),连接OP.
(1)求反比例函数y=![]() (m≠0)的表达式;
(m≠0)的表达式;
(2)若△AOB的面积是△POB的面积的2倍,求直线y=kx+b的表达式.
【答案】(1)y=![]() ;(2) y=﹣3x+6或y=x+2.
;(2) y=﹣3x+6或y=x+2.
【解析】分析:(1)把点P坐标代入反比例函数关系式y=![]() 即可求出m的值;
即可求出m的值;
(2)先根据△AOB的面积是△POB的面积的2倍求出点A的坐标,再用待定系数法求出一次函数解析式即可.
详解:(1)∵反比例函数y=![]() (m≠0)的图象经过点P(1,3),
(m≠0)的图象经过点P(1,3),
∴m=1×3=3,
∴反比例函数的表达式为y=![]() ;
;
(2)过P作PE⊥y轴于E,则PE=1.
∵△AOB的面积是△POB的面积的2倍,
∴![]() OBOA=
OBOA=![]() OBPE×2,
OBPE×2,
∴OA=2PE=2,
∴A(2,0)或A(﹣2,0).
①当A点坐标为(2,0)时,如图1.
将A(2,0)、P(1,3)代入y=kx+b,
得![]() ,解得
,解得![]() ,
,
∴直线AB的表达式为y=﹣3x+6;
②当A点坐标为(﹣2,0)时,如图2.
将A(﹣2,0)、P(1,3)代入y=kx+b,
得![]() ,解得
,解得![]() ,
,
∴直线AB的表达式为y=x+2.
综上可知,直线AB的表达式为y=﹣3x+6或y=x+2.

【题目】权威市调机构IDC发布了2018年第四季度全球智能手机出货量报告如下表:
手机品牌 | 2018年第四季度市场出货量(万台) | 2018年第四季度市场份额 | 2017年第四季度市场出货量(万台) | 2017年第四季度市场份额 |
Samsung | 70.4 | 18.7% | 74.5 | 18.9% |
Apple | 68.4 | 18.2% | 77.3 | 19.6% |
Huawei | 60.5 | 16.1% | 42.1 | 10.7% |
Xiaomi | 29.2 | 7.8% | 27.3 | 6.9% |
HMDGlobal | 28.6 | 7.6% | 28.2 | 7.1% |
Others | 118.4 | 31.5% | 145.3 | 36.8% |
总计 | 75.4 | 100.0% | 394.6 | 100.0% |
根据上表数据得出以下推断,其中结论正确的是( )
A.Huawei和Xiaomi2018年第四季度市场份额总和达到25%
B.2018年第四季度比2017年第四季度市场份额增幅最大的是Apple手机
C.Huawei手机2018年第四季度比2017年第四季度市场出货量增加18.4万合
D.2018年第四季度全球智能手机出货量同比下降约10%