Question

【题目】已知一次函数（k≠0）的图象经过， 两点，二次函数（其中a＞2）.

（1）求一次函数的表达式及二次函数图象的顶点坐标（用含a的代数式表示）；

（2）利用函数图象解决下列问题：

①若，求当且≤0时，自变量x的取值范围；

②如果满足且≤0时的自变量x的取值范围内恰有一个整数，直接写出a的取值范围.

Answer 1

【答案】（1）；二次函数图象的顶点坐标为；（2）①2＜x≤4.②≤a＜.

【解析】（1）根据待定系数法即可求得一次函数的解析式；把y2=x2-2ax+4通过配方转化成顶点式即可求得顶点坐标．

（2）①当a=时，y2=x2-5x+4，画出函数的图象，根据图象即可求得自变量x的取值范围；

②根据题意结合图象可知x=3，把x=3代入y2=x2-2ax+4≥0即可求得a的取值；

解：（1）∵ 一次函数（k≠0）的图象经过， 两点，

∴

解得

∴.

∵，

∴ 二次函数图象的顶点坐标为；

（2）①当时， ，

如图,

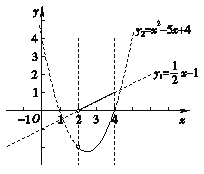
因为y1>0且y20，由图象得2<x4.

②由①可知a=时，2<x4有两个整数，

∴a<，

∵如果满足y1>0且y20时的自变量x的取值范围内恰有一个整数，

∴x=3，

当x=3时,y2=x22ax+40，

解得a，

∴a<.