题目内容
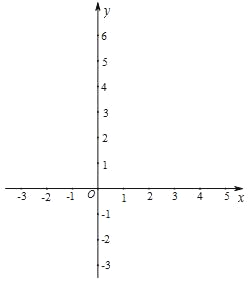
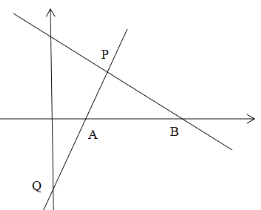
【题目】在平面直角坐标系中，直线y1=kx+b经过点P（2，2）和点Q（0，﹣2），与x轴交于点A，与直线y2=mx+n交于点P．
（1）求出直线y1=kx+b的解析式；
（2）当m＜0时，直接写出y1＜y2时自变量x的取值范围；
（3）直线y2=mx+n绕着点P任意旋转，与x轴交于点B，当△PAB是等腰三角形时，点B有几种位置？请你分别求出点B的坐标．
【答案】（1）y1=2x－2（2）x＜2（3）（
+1，0）、（3，0）、（3.5，0）、（1－，0）
【解析】
（1）运用待定系数法求解即可；
（2）根据m＜0时，由函数图象即可确定当y1＜y2时自变量x的取值范围；
（3）分m＞0时和m＜0时两种情况进行讨论，根据等腰三角形的性质确定点B的位置即可.
（1）把P（2，2）和点Q（0，﹣2）代入y1=kx+b得，
，解得
，
所以，直线的解析式为：y1=2x－2
（2）当m＜0时，由图象得，y1＜y2时自变量x的取值范围x＜2；
（3）过点P作PM⊥x轴，交于点M
由题意可知A（1，0），M（2，0），AP=，AM=1
当m＞0时，点B有3种位置使得△PAB为等腰三角形
①当AP=AB时，AB=，∴B（+1，0）
②当PA=PB时，AB=2AM=2，∴B（3，0）
③当BA=BP时，设AB=x，由等面积法可得S△ABP=2x=
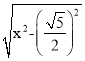
解得x=2.5，∴B（3.5，0）
当m＜0时，点B有1种位置使得△PAB为等腰三角形
当AB=AP时，OB=－1，∴B（1－，0）
综上所述，点B有4种位置使得△PAB为等腰三角形，坐标分别为（+1，0）、（3，0）、（3.5，0）、（1－，0）
阅读快车系列答案
【题目】某学习兴趣小组参加一次单元测验，成绩统计情况如下表．
分 数 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 82 | 83 | 84 | 86 | 88 | 90 | 92 |
人 数 | 1 | 1 | 5 | 4 | 3 | 2 | 3 | 1 | 1 | 1 | 2 | 3 | 1 | 2 |
（1）该兴趣小组有多少人？
（2）兴趣小组本次单元测试成绩的平均数、中位数、众数各是多少？
（3）老师打算为兴趣小组下单元考试设定一个新目标，学生达到或超过目标给予奖励，并希望小组 三分之一左右的优秀学生得到奖励，请你帮老师从平均数、中位数、众数三个数中选择一个比较恰 当的目标数；如果计划让一半左右的人都得到奖励，确定哪个数作为目标恰当些？
