题目内容
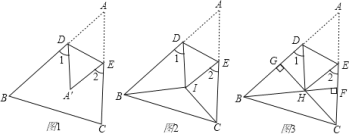
【题目】(1)如图1,把△ABC沿DE折叠,使点A落在点A’处,若∠A=50°,求∠1+∠2的度数,猜想并直接写出∠1+∠2与∠A的数量关系.(不必证明)
(2)如图2,BI平分∠ABC,CI平分∠ACB,把△ABC折叠,使点A与点I重合,若∠1+∠2=110°,求∠BIC的度数;
(3)如图3,在锐角△ABC中,BF⊥AC于点F,CG⊥AB于点G,BF、CG交于点H,把△ABC折叠使点A和点H重合,试探索∠BHC与∠1+∠2的关系,并证明你的结论.
【答案】(1)100°,∠1+∠2=2∠A;(2)117.5°;(3)∠BHC=180°-![]() (∠1+∠2),证明见解析.
(∠1+∠2),证明见解析.
【解析】
(1)根据翻折变换的性质以及三角形内角和定理以及平角的定义求出即可;
(2)根据三角形角平分线的性质得出∠IBC+∠ICB=90°-![]() ∠A,得出∠BIC的度数即可;
∠A,得出∠BIC的度数即可;
(3)根据翻折变换的性质以及垂线的性质得出,∠AFH+∠AGH=90°+90°=180°,进而求出∠A=![]() (∠1+∠2),即可得出答案.
(∠1+∠2),即可得出答案.
(1)∠1+∠2=2∠A;
理由:根据翻折的性质,∠ADE=![]() (180°-∠1),∠AED=
(180°-∠1),∠AED=![]() (180°-∠2),
(180°-∠2),
∵∠A+∠ADE+∠AED=180°,
∴∠A+![]() (180-∠1)+
(180-∠1)+![]() (180-∠2)=180°,
(180-∠2)=180°,
整理得2∠A=∠1+∠2,
∵∠A=50°,
∴∠1+∠2=100°,
猜想:∠1+∠2=2∠A;
(2)由(1)∠1+∠2=2∠A,得2∠A=110°,∴∠A=55°,
∵IB平分∠ABC,IC平分∠ACB,
∴∠IBC+∠ICB=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() (180°-∠A)=90°-
(180°-∠A)=90°-![]() ∠A,
∠A,
∴∠BIC=180°-(∠IBC+∠ICB)=180°-(90°-![]() ∠A)=90°+
∠A)=90°+![]() ×55°=117.5°;
×55°=117.5°;
(3)∵BF⊥AC,CG⊥AB,
∴∠AFH+∠AGH=90°+90°=180°,
∴∠FHG+∠A=360°-180°=180°,
∴∠BHC=∠FHG=180°-∠A,
由(1)知∠1+∠2=2∠A,
∴∠A=![]() (∠1+∠2),
(∠1+∠2),
∴∠BHC=180°-![]() (∠1+∠2).
(∠1+∠2).