Question

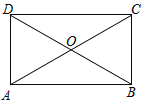
【题目】已知：矩形ABCD中，对角线AC与BD交于点O，∠BOC=120°，AC=4cm，求矩形ABCD的周长．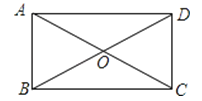

Answer 1

【答案】解：∵四边形ABCD是矩形，
∴AB=DC，AD=BC，∠ABC=90°，OA=OB=AC=2cm，
∵∠BOC=120°，
∴∠AOB=60°，
∴△AOB是等边三角形，
∴AB=OA=2cm，
∴AD=BC===2（cm），
∴矩形ABCD的周长=2（AB+BC）=4+4（cm）．
【解析】由矩形的性质得出AB=DC，AD=BC，∠ABC=90°，OA=OB=AC，证明△AOB是等边三角形，得出AB=OA=2cm，再由勾股定理求出BC，即可得出矩形ABCD的周长．
【考点精析】掌握矩形的性质是解答本题的根本，需要知道矩形的四个角都是直角，矩形的对角线相等．