Question

【题目】A，B两地被大山阻隔，若要从A地到B地，只能沿着如图所示的公路先从A地到C地，再由C地到B地．现计划开凿隧道A，B两地直线贯通，经测量得：∠CAB=30°，∠CBA=45°，AC=20km，求隧道开通后与隧道开通前相比，从A地到B地的路程将缩短多少？（结果精确到0.1km，参考数据： ≈1.414， ≈1.732）

Answer 1

【答案】解：过点C作CD⊥AB与D，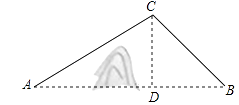

∵AC=10km，∠CAB=30°，
∴CD= AC= ×20=10km，
AD=cos∠CABAC=cos∠30°×20=10 km，
∵∠CBA=45°，
∴BD=CD=10km，BC= CD=10 ≈14.14km，
∴AB=AD+BD=10 +10≈27.32km，
则AC+BC﹣AB≈20+14.14﹣27.32≈6.8km，
答：从A地到B地的路程将缩短6.8km
【解析】过点C作CD⊥AB于D，根据AC=20km，∠CAB=30°，求出CD、AD，根据∠CBA=45°，求出BD、BC，最后根据AB=AD+BD列式计算即可．