ΧβΡΩΡΎ»ί
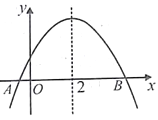
ΓΨΧβΡΩΓΩ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§≈ΉΈοœΏ![]() ”κx÷αΫΜ”ΎAΓΔBΘ®AΒψ‘ΎBΒψΒΡΉσ≤ύΘ©”κy÷αΫΜ”ΎΒψCΓΘ
”κx÷αΫΜ”ΎAΓΔBΘ®AΒψ‘ΎBΒψΒΡΉσ≤ύΘ©”κy÷αΫΜ”ΎΒψCΓΘ
Θ®1Θ©»γΆΦ1Θ§Ν§Ϋ”ACΓΔBCΘ§«σΓςABCΒΡΟφΜΐΓΘ
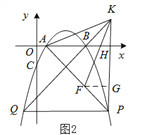
Θ®2Θ©»γΆΦ2ΘΚ
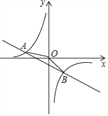
ΔΌΙΐΒψCΉςCRΓΈx÷αΫΜ≈ΉΈοœΏ”ΎΒψRΘ§«σΒψRΒΡΉχ±ξΘΜ
ΔΎΒψPΈΣΒΎΥΡœσœό≈ΉΈοœΏ…œ“ΜΒψΘ§Ν§Ϋ”PCΘ§»τΓœBCP=2ΓœABC ±Θ§«σΒψPΒΡΉχ±ξΓΘ
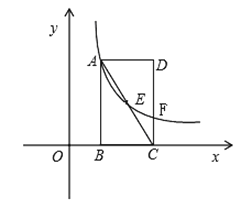
Θ®3Θ©»γΆΦ3Θ§‘ΎΘ®2Θ©ΒΡΧθΦΰœ¬Θ§ΒψF‘ΎAP…œΘ§ΙΐΒψPΉςPHΓΆx÷α”ΎHΒψΘ§ΒψK‘ΎPHΒΡ―”≥ΛœΏ…œΘ§AK=KFΘ§ΓœKAH=ΓœFKHΘ§PF=![]() Θ§Ν§Ϋ”KB≤Δ―”≥ΛΫΜ≈ΉΈοœΏ”ΎΒψQΘ§«σPQΒΡ≥ΛΓΘ
Θ§Ν§Ϋ”KB≤Δ―”≥ΛΫΜ≈ΉΈοœΏ”ΎΒψQΘ§«σPQΒΡ≥ΛΓΘ
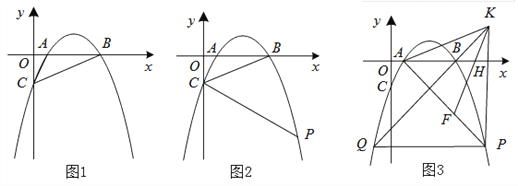
ΓΨ¥πΑΗΓΩΘ®1Θ©3Θ®2Θ©ΔΌQΘ®-2Θ§5Θ©ΔΎ6Θ®3Θ©7
ΓΨΫβΈωΓΩΖ÷ΈωΘΚΘ®1Θ©Ννy=0Θ§Φ¥![]() =0Θ§ΒΟΒψAΘ§BΒΡΉχ±ξΘ§Ννx=0«σ≥ωΒψCΒΡΉχ±ξΘ§»ΜΚσΗυΨί»ΐΫ«–ΈΟφΜΐΙΪ Ϋ«σ≥ωΓςABCΒΡΟφΜΐΘΜ
=0Θ§ΒΟΒψAΘ§BΒΡΉχ±ξΘ§Ννx=0«σ≥ωΒψCΒΡΉχ±ξΘ§»ΜΚσΗυΨί»ΐΫ«–ΈΟφΜΐΙΪ Ϋ«σ≥ωΓςABCΒΡΟφΜΐΘΜ
Θ®2Θ©ΔΌ”…CRΓΈx÷αΩ…÷ΣΒψRΒΡΉίΉχ±ξ «-2Θ§…ηRΘ®qΘ§-2Θ©Θ§Α―RΘ®qΘ§-2Θ©¥ζ»κΕΰ¥ΈΚ· ΐΫβΈω ΫΦ¥Ω…«σ≥ωΒψRΒΡΉχ±ξΘΜΔΎ”…Χβ“βΩ…÷ΣΘ§Β±ΓœPCR=ΓœBCR ±Θ§ΒψPΦ¥Υυ«σ. ―”≥ΛPCΫΜx÷α”ΎΒψD,”…ΓςDOCΓ’ΓςBOC«σ≥ωΒψDΒΡΉχ±ξΘ§ΫχΕχ«σ≥ω÷±œΏCDΒΡΫβΈω ΫΘ§»ΜΚσΝΣΝΔΕΰ¥ΈΚ· ΐΚΆΥυ«σ“Μ¥ΈΚ· ΐΫβΈω ΫΦ¥Ω…«σ≥ωΒψPΒΡΉχ±ξΘΜ
Θ®3Θ©ΉςFGΓΆPKΘ§œ»÷ΛΟςΓœHAP=ΓœKPAΘ§ΒΟHA=HPΘ§”…ΓςAKHΓ’ΓςKFGΘ§Ω…ΒΟKH=FG=2Θ§ΫχΕχΒΟ≥ωKΒΡΉχ±ξΘ§‘Ό”…¥ΐΕ®œΒ ΐΖ®«σ≥ω÷±œΏKBΒΡΙΊœΒ ΫΘ§≤Δ”κΕΰ¥ΈΚ· ΐΙΊœΒ ΫΝΣΝΔΘ§«σ≥ωΖΫ≥ΧΉιΒΡΫβΘ§ΫαΚœPQΓΈx÷αΦ¥Ω…ΒΟ≥ω¥πΑΗ.
œξΫβΘΚΘ®1Θ©Ννy=0Θ§ΒΟ![]() =0Θ§
=0Θ§
Ϋβ÷°ΒΟΘ§
x1=1,x2=4,
ΓύA(1,0)Θ§BΘ®4.0Θ©;
Ννx=0ΒΟΘ§
![]() Θ§
Θ§
ΓύCΘ®0Θ§-2Θ©.
Γύ ![]() =3
=3
Θ®2Θ©ΔΌ ΓΏ CRΓΈx÷α
Γύ Ω……ηRΘ®qΘ§-2Θ©
‘ρΘΚ![]()
ΫβΒΟΘΚq1=0Θ§q2=5
Γύ RΘ®-2Θ§5Θ©
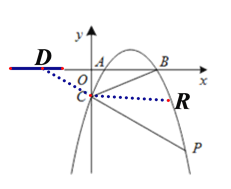
ΔΎΒ±ΓœPCR=ΓœBCR ±Θ§ΒψPΦ¥Υυ«σΓΘ
―”≥ΛPCΫΜx÷α”ΎΒψD,
ΓΏ CRΓΈx÷α,
ΓύΓœPDB=ΓœPCR.
ΓΏΓœABC=ΓœBCR=ΓœPCR,
ΓύΓœPDB=ΓœABC.
”÷ΓΏOC=OCΘ§ΓœDOC=ΓœBOC=90Γψ,
ΓύΓςDOCΓ’ΓςBOC,
ΓύOD=OB,
ΓύDΘ®-4,0Θ©,
ΓύyCD=![]() ,
,
ΫβΖΫ≥ΧΉιΘΚ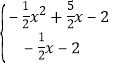 ΒΟΘΚ
ΒΟΘΚ
![]() Θ§
Θ§![]() ,
,
Γύ ΒψPΒΡΚαΉχ±ξ «6 ;
Θ®3Θ©ΙΐΒψFΉςFGΓΆPK”ΎΒψGΘ§
ΓΏ AK=FK
Γύ ΓœKAF=ΓœKFA
ΕχΓœKAF=ΓœKAH+ΓœPAHΘ§ΓœKFA=ΓœPKF+ΓœKPFΘ§
”…Χβ“βΓœKAH=ΓœFKPΘ§
ΓύΓœHAP=ΓœKPAΘ§
ΓύHA=HPΘ§
ΓύΓςAHPΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–Έ
ΓύΓœFPG=45Γψ
ΓύΓςFPGΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–Έ
ΓύFG=PG=![]() =2
=2
‘ΎΓςAKHΚΆΓςKFG÷–
ΓΏΓœAHK=ΓœKGF=90ΓψΘ§ΓœKAH=ΓœFKGΘ§KA=FK
ΓύΓςAKHΓ’ΓςKFGΘ®AASΘ©
ΓύKH=FG=2
ΓύKΘ®6,2Θ©
”÷ ΓΏ BΘ®4,0Θ©
ΓύyKB=x-4
ΫβΖΫ≥ΧΉι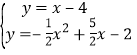 ΒΟ
ΒΟ![]() Μρ
Μρ![]()
ΓύQΘ®-1Θ§-5Θ©
ΕχPΘ®6Θ§-5Θ©
ΓύPQΓΈx÷α
ΓύPQ=7

 ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ
ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ –Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
–Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ