题目内容
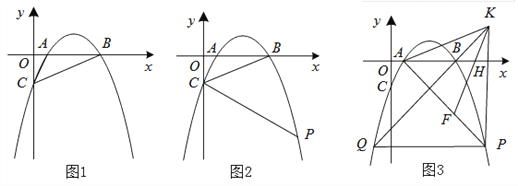
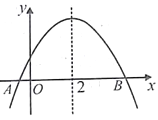
【题目】如图,已知二次函数![]() 图象与x轴交于A,B两点,对称轴为直线x=2,下列结论:①abc>0; ②4a+b=0;③若点A坐标为(1,0),则线段AB=5; ④若点M(x1,y1)、N(x2,y2)在该函数图象上,且满足0<x1<1,2<x2<3,则y1<y2其中正确结论的序号为( )
图象与x轴交于A,B两点,对称轴为直线x=2,下列结论:①abc>0; ②4a+b=0;③若点A坐标为(1,0),则线段AB=5; ④若点M(x1,y1)、N(x2,y2)在该函数图象上,且满足0<x1<1,2<x2<3,则y1<y2其中正确结论的序号为( )
A. ①,② B. ②,③ C. ③,④ D. ②,④
【答案】D
【解析】解:∵抛物线开口向下,∴a<0.∵对称轴![]() ,∴b=-4a>0.∵抛物线与y轴交点在y轴正半轴,∴c>0,∴abc<0,故①错误;
,∴b=-4a>0.∵抛物线与y轴交点在y轴正半轴,∴c>0,∴abc<0,故①错误;
由①得:b=-4a,∴4a+b=0,故②正确;
若点A坐标为(1,0),因为对称轴为x=2,∴B(5,0),∴AB=5+1=6.故③错误;
∵a<0,∴横坐标到对称轴的距离越大,函数值越小.∵0<x1<1,2<x2<3,∴ ![]() ,∴y1<y2,故④正确.
,∴y1<y2,故④正确.
故选D.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目