题目内容
【题目】如图,已知![]() ,射线
,射线![]() .
.
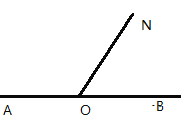
![]() 请画出
请画出![]() 的平分线
的平分线![]() ;
;
![]() 如果
如果![]() ,射线
,射线![]() 分别表示从点
分别表示从点![]() 出发东、西两个方向,那么射线
出发东、西两个方向,那么射线![]() 方向,射线
方向,射线![]() 表示 方向.
表示 方向.
![]() 在
在![]() 的条件下,当
的条件下,当![]() 时,在图中找出所有与
时,在图中找出所有与![]() 互补的角,这些角是_ .
互补的角,这些角是_ .
【答案】(1)详见解析;(2)北偏东20°,北偏西35°;(3)![]()
【解析】
(1)以点O为圆心,以任意长为半径画弧,与OB、ON相交于两点,再分别以这两点为圆心,以大于它们![]() 长度为半径画弧,两弧相交于一点,然后过点O与这点作射线OC即为所求;
长度为半径画弧,两弧相交于一点,然后过点O与这点作射线OC即为所求;
(2)过点O作OE⊥AB,根据垂直的定义以及角平分线的定义求出∠EON与∠COE,然后根据方位角的定义解答即可;
(3)根据∠AON=60°,利用平角的定义可得∠BON,利用角平分线的定义求出∠CON=60°,然后求出∠AOC=120°从而得解.
解:(1)如图所示,OC即为∠BON的平分线;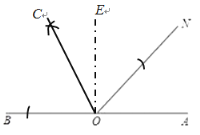
(2)过点O作OE⊥AB,
∵∠AON=70°,
∴∠EON=90°-70°=20°,
∴ON是北偏东20°,
∵OC平分∠BON,
∴∠CON=![]() (180°-70°)=55°,
(180°-70°)=55°,
∴∠COE=∠CON-∠EON=55°-20°=35°,
∴OC是北偏西35°;
故答案为:北偏东20°;北偏西35°.
(3)∵∠AON=60°,OC平分∠BON,
∴∠CON=![]() (180°-60°)=60°,
(180°-60°)=60°,
∴∠AOC=∠CON+∠AON=60°+60°=120°,
∴∠AOC+∠AON=180°,
又根据平角的定义得,∠BON+∠AON=180°,
∴与∠AON互补的角有∠AOC,∠BON;
故答案为:∠AOC,∠BON.

练习册系列答案
相关题目