题目内容
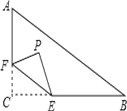
【题目】如图,M是ΔABC的边BC的中点,AN平分![]() BAC, BN
BAC, BN![]() AN于点N延长BN交AC于点D,已知AB=10,BC=15,MN=3
AN于点N延长BN交AC于点D,已知AB=10,BC=15,MN=3
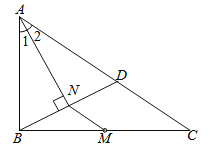
(1)求证:ΔBAN≌ΔDAN
(2)求ΔABC的周长
【答案】(1)详见解析;(2)41
【解析】
(1)根据题意∠1=∠2,AN=AN,∠ANB=∠AND=90°,即可证明ΔBAN≌ΔDAN;
(2)由(1)可知,AB=AD,N为BD的中点,则MN为中位线,得CD=2MN,然后计算可得周长.
解:(1)∵AN平分![]() BAC,
BAC,
∴∠1=∠2,
∵BN![]() AN,
AN,
∴∠ANB=∠AND=90°,
∵AN=AN,
∴ΔBAN≌ΔDAN(ASA);
(2)由ΔBAN≌ΔDAN,
∴AB=AD,BN=DN,
∴N为BD的中点,
∵M是ΔABC的边BC的中点,
∴MN为△BCD的中位线,
∴CD=2MN=6,
∵AB=AD=10,BC=15,
∴ΔABC的周长=AB+BC+AC=AB+BC+AD+DC=10+15+10+6=41.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目