Question

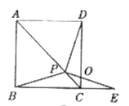
【题目】如图，在正方形ABCD中，P是对角线AC上的一点，点E在BC的延长线上，且PE=PB，PE与DC交于点O．

（基础探究）

（1）求证：PD=PE．

（2）求证：∠DPE=90°

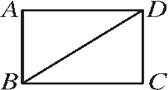
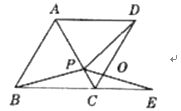
（3）（应用拓展）把正方形ABCD改为菱形，其他条件不变(如图)，若PE=3，则PD=________；

若∠ABC=62°，则∠DPE=________.

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）,.

【解析】

（1）由正方形的性质可得DC=BC，∠ACB=∠ACD，利用SAS证明△PBC≌△PDC，根据全等三角形的性质可得PD=PB，又因PE=PB,即可证得PD=PE；（2）类比（1）的方法证明△PBC≌△PDC，即可得∠PDC=∠PBC.再由PE=PB，根据等腰三角形的性质可得∠PBC=∠E，所以∠PDC=∠E.因为∠POD=∠COE，根据三角形的内角和定理可得∠DPO=∠OCE=90；（3）类比（1）的方法证得PD=PE=3；类比（2）的方法证得∠DPE=∠DCE，由平行线的性质可得∠ABC=∠DCE=62°，由此可得∠DPE=62°.

（1）证明：在正方形ABCD中，DC=BC，∠ACB=∠ACD，

在△PBC和△PDC中，

∵DC=BC，∠ACB=∠ACD（已证），CP=CP（公共边），

∴△PBC≌△PDC.

∴PD=PB.

又∵PE=PB,

∴PD=PE；

（2）证明：在正方形ABCD中，DC=BC，∠ACB=∠ACD，

在△PBC和△PDC中，

∵DC=BC，∠ACB=∠ACD（已证），,CP=CP（公共边）

∴△PBC≌△PDC.

∴∠PDC=∠PBC.

又∵PE=PB，∴∠PBC=∠E.

∴∠PDC=∠E.

又∵∠POD=∠COE,

∴∠DPO=∠OCE=90；

（3）在菱形ABCD中，DC=BC，∠ACB=∠ACD，

在△PBC和△PDC中，

∵DC=BC，∠ACB=∠ACD（已证），,CP=CP（公共边）

∴△PBC≌△PDC.

∴∠PDC=∠PBC，PD=PB.

又∵PE=PB，

∴∠PBC=∠E， PD=PE=3.

∴∠PDC=∠E.

又∵∠POD=∠COE,

∴∠DPE=∠DCE；

∵AB∥CD，∠ABC=62°，

∴∠ABC=∠DCE=62°，

∴∠DPE=62°.

故答案为：3，62°.