题目内容
【题目】已知关于x的一元二次方程![]() 有实数根.
有实数根.
(1)求m的值;
(2)先作![]() 的图象关于x轴的对称图形,然后将所作图形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式;
的图象关于x轴的对称图形,然后将所作图形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式;
(3)在(2)的条件下,当直线y=2x+n(n≥m)与变化后的图象有公共点时,求![]() 的最大值和最小值.
的最大值和最小值.
【答案】(1)1;(2)![]() ;(3)最大值为21,最小值为﹣4.
;(3)最大值为21,最小值为﹣4.
【解析】
试题(1)由题意△≥0,列出不等式,解不等式即可;
(2)画出翻折.平移后的图象,根据顶点坐标即可写出函数的解析式;
(3)首先确定n的取值范围,利用二次函数的性质即可解决问题;
试题解析:(1)对于一元二次方程![]() ,△=(m+1)2﹣2(m2+1)=﹣m2+2m﹣1=﹣(m﹣1)2,∵方程有实数根,∴﹣(m﹣1)2≥0,∴m=1.
,△=(m+1)2﹣2(m2+1)=﹣m2+2m﹣1=﹣(m﹣1)2,∵方程有实数根,∴﹣(m﹣1)2≥0,∴m=1.
(2)由(1)可知![]() =
=![]() ,图象如图所示:
,图象如图所示:
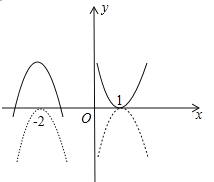
平移后的解析式为![]() ,即
,即![]() .
.
(3)由![]() 消去y得到
消去y得到![]() ,由题意△≥0,∴36﹣4n﹣8≥0,∴n≤7,∵n≤m,m=1,∴1≤n≤7,令y′=n2﹣4n=(n﹣2)2﹣4,∴n=2时,y′的值最小,最小值为﹣4,n=7时,y′的值最大,最大值为21,∴
,由题意△≥0,∴36﹣4n﹣8≥0,∴n≤7,∵n≤m,m=1,∴1≤n≤7,令y′=n2﹣4n=(n﹣2)2﹣4,∴n=2时,y′的值最小,最小值为﹣4,n=7时,y′的值最大,最大值为21,∴![]() 的最大值为21,最小值为﹣4.
的最大值为21,最小值为﹣4.

练习册系列答案
相关题目



