ЬтФПФкШн
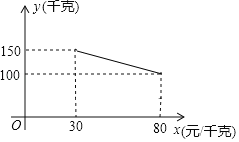
ЁОЬтФПЁПФГГЌЪаЯњЪлвЛжжЩЬЦЗЃЌГЩБОМлЮЊ20дЊ/ЧЇПЫЃЌОЪаГЁЕїВщЃЌУПЬьЯњЪлСПy(ЧЇПЫ)гыЯњЪлЕЅМлx(дЊЧЇПЫ)жЎМфЕФЙиЯЕШчЭМЫљЪОЃЌЙцЖЈУПЧЇПЫЪлМлВЛФмЕЭгк30дЊЃЌЧвВЛИпгк80дЊЃЎ
(1)жБНгаДГіyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
(2)ШчЙћИУГЌЪаЯњЪлетжжЩЬЦЗУПЬьЛёЕУ3900дЊЕФРћШѓЃЌФЧУДИУЩЬЦЗЕФЯњЪлЕЅМлЮЊЖрЩйдЊЃП
(3)ЩшУПЬьЕФзмРћШѓЮЊwдЊЃЌЕБЯњЪлЕЅМлЖЈЮЊЖрЩйдЊЪБЃЌИУГЌЪаУПЬьЕФРћШѓзюДѓЃПзюДѓРћШѓЪЧЖрЩйдЊЃП
ЁОД№АИЁП(1)yЃНЉx+180ЃЛ(2)ИУЩЬЦЗЕФЯњЪлЕЅМлЮЊ50дЊЃЛ(3)ЯњЪлЕЅМлЖЈЮЊ80дЊЪБЃЌИУГЌЪаУПЬьЕФРћШѓзюДѓЃЌзюДѓРћШѓ6000дЊЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉНЋЕуЃЈ30ЃЌ150ЃЉЁЂЃЈ80ЃЌ100ЃЉДњШывЛДЮКЏЪ§БэДяЪНЃЌМДПЩЧѓНтЃЛ
ЃЈ2ЃЉгЩЬтвтЕУЃКЃЈx20ЃЉЃЈxЃЋ180ЃЉЃН3900ЃЌМДПЩЧѓНтЃЛ
ЃЈ3ЃЉгЩЬтвтЕУЃКwЃНЃЈx20ЃЉЃЈxЃЋ180ЃЉЃНЃЈx100ЃЉ2ЃЋ6400ЃЌМДПЩЧѓНтЃЎ
НтЃК(1)НЋЕу(30ЃЌ150)ЁЂ(80ЃЌ100)ДњШывЛДЮКЏЪ§БэДяЪНЕУЃК![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
ЙЪКЏЪ§ЕФБэДяЪНЮЊЃКyЃНЉx+180ЃЛ
(2)гЩЬтвтЕУЃК(xЉ20)(Љx+180)ЃН3900ЃЌ
НтЕУЃКxЃН50Лђ150(ЩсШЅ150)ЃЌ
ЙЪЃКИУЩЬЦЗЕФЯњЪлЕЅМлЮЊ50дЊЃЛ
(3)гЩЬтвтЕУЃКwЃН(xЉ20)(Љx+180)ЃНЉ(xЉ100)2+6400ЃЌ
ЁпЉ1ЃМ0ЃЌЙЪЕБxЃМ100ЪБЃЌWЫцxЕФдіДѓЖјдіДѓЃЌЖј30ЁмxЁм80ЃЌ
ЁрЕБxЃН80ЪБЃЌWгЩзюДѓжЕЃЌДЫЪБЃЌwЃН6000ЃЌ
ЙЪЯњЪлЕЅМлЖЈЮЊ80дЊЪБЃЌИУГЌЪаУПЬьЕФРћШѓзюДѓЃЌзюДѓРћШѓ6000дЊЃЎ

 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИЁОЬтФПЁППьЕнЙЋЫОЮЊЬсИпПьЕнЗжМ№ЕФЫйЖШЃЌОіЖЈЙКТђЛњЦїШЫРДДњЬцШЫЙЄЗжМ№ЃЌСНжжаЭКХЕФЛњЦїШЫЕФЙЄзїаЇТЪКЭМлИёШчБэЃК
аЭКХ | Мз | вв |
УПЬЈУПаЁЪБЗжМ№ПьЕнМўЪ§(Мў) | 1000 | 800 |
УПЬЈМлИё(ЭђдЊ) | 5 | 3 |
ИУЙЋЫОМЦЛЎЙКТђетСНжжаЭКХЕФЛњЦїШЫЙВ10ЬЈЃЌВЂЧвЪЙет10ЬЈЛњЦїШЫУПаЁЪБЗжМ№ПьЕнМўЪ§змКЭВЛЩйгк8500Мў
(1)ЩшЙКТђМзжжаЭКХЕФЛњЦїШЫxЬЈЃЌЙКТђет10ЬЈЛњЦїШЫЫљЛЈЕФЗбгУЮЊyЭђдЊЃЌЧѓyгыxжЎМфЕФЙиЯЕЪНЃЛ
(2)ЙКТђМИЬЈМзжжаЭКХЕФЛњЦїШЫЃЌФмЪЙЙКТђет10ЬЈЛњЦїШЫЫљЛЈзмЗбгУзюЩйЃПзюЩйЗбгУЪЧЖрЩйЃП
ЁОЬтФПЁПЮЊСЫЙФРјГЧЪажмБпЕФХЉУёЕФжжВЫЕФЛ§МЋадЃЌФГЙЋЫОМЦЛЎаТНЈ![]() ЃЌ
ЃЌ![]() СНжжЮТЪв80ЖАЃЌНЋЦфЪлИјХЉУёжжВЫЃЎвбжЊНЈ1Иі
СНжжЮТЪв80ЖАЃЌНЋЦфЪлИјХЉУёжжВЫЃЎвбжЊНЈ1Иі![]() аЭЮТЪвКЭ2Иі
аЭЮТЪвКЭ2Иі![]() аЭЮТЪввЛЙВашвЊ8.1ЭђдЊЃЌСНжжЮТЪвЕФГЩБОКЭГіЪлМлШчЯТБэЃК
аЭЮТЪввЛЙВашвЊ8.1ЭђдЊЃЌСНжжЮТЪвЕФГЩБОКЭГіЪлМлШчЯТБэЃК
|
| |
ГЩБОЃЈЭђдЊ/ЖАЃЉ | 2.5 |
|
ГіЪлМлЃЈЭђдЊ/ЖАЃЉ | 3.1 | 3.5 |
ЃЈ1ЃЉЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉвбжЊаТНЈ![]() аЭЮТЪвВЛЩйгк38ЖАВЛЖргк50ЖАЧвЫљНЈЕФСНжжЮТЪвПЩШЋВПЪлГіЃЎЮЊСЫМѕЧсВЫХЉИКЕЃЃЌЪдЮЪВЩгУЪВУДЗНАИНЈЩшЮТЪвПЩЪЙРћШѓзюЩйЃЌзюЩйРћШѓЪЧЖрЩйЃП
аЭЮТЪвВЛЩйгк38ЖАВЛЖргк50ЖАЧвЫљНЈЕФСНжжЮТЪвПЩШЋВПЪлГіЃЎЮЊСЫМѕЧсВЫХЉИКЕЃЃЌЪдЮЪВЩгУЪВУДЗНАИНЈЩшЮТЪвПЩЪЙРћШѓзюЩйЃЌзюЩйРћШѓЪЧЖрЩйЃП