题目内容
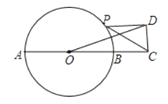
【题目】如图,线段AB为⊙O的直径,点C在AB的延长线上,AB=4,BC=2,点P是⊙O上一动点,连接CP,以CP为斜边在PC的上方作Rt△PCD,且使∠DCP=60°,连接OD,则OD长的最大值为 ( )
A.![]() B.
B.![]() C.
C.![]() D.4
D.4
【答案】C
【解析】
如图,作△COE,使得∠CEO=90°,∠ECO=60°,则CO=2CE,OE=2![]() ,∠OCP=∠ECD,由△COP∽△CED,推出
,∠OCP=∠ECD,由△COP∽△CED,推出![]() =
=![]() =2,即ED=
=2,即ED=![]() OP=1(定长),由点E是定点,DE是定长,推出点D在半径为1的⊙E上,由此即可解决问题.
OP=1(定长),由点E是定点,DE是定长,推出点D在半径为1的⊙E上,由此即可解决问题.
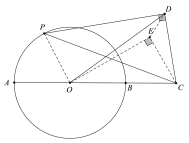
解:如图,作△COE,使得∠CEO=90°,∠ECO=60°,则CO=2CE,OE=2![]() ,
,
∠OCP=∠ECD,
∵∠CDP=90°,∠DCP=60°,
∴CP=2CD,
∴![]() =
=![]() =2,
=2,
∴△COP∽△CED,
∴![]() =
=![]() =2,
=2,
即ED=![]() OP=1(定长),
OP=1(定长),
∵点E是定点,DE是定长,
∴点D在半径为1的⊙E上,
∵OD≤OE+DE=2![]() +1,
+1,
∴OD的最大值为2![]() +1,
+1,
故选C.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目