题目内容
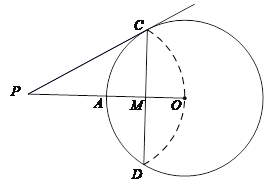
【题目】如图,已知⊙O的半径为4,OA为半径,CD为弦,OA与CD交于点M,将弧CD沿着CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,连接PC.
(1)求CD的长;
(2)求证:PC是⊙O的切线.
【答案】(1)4![]() (2) PC与☉O相切
(2) PC与☉O相切
【解析】(1)连接OC,根据翻折的性质求出OM,CD⊥OA,再利用勾股定理列式求解即可;
(2)利用勾股定理列式求出PC,然后利用勾股定理逆定理求出∠PCO=90°,再根据圆的切线的定义证明即可,
(1)连接OC,
∵弧CD沿CD翻折后,A与O重合,
∴OM=![]() OA=2,CD⊥OA
OA=2,CD⊥OA
∵OC=4,
∴CD=2CM=2![]() =4
=4![]() ;
;
(2)∵PA=OA=4,AM=OM=2,CM=2![]() ,PM=PA+AM=6,
,PM=PA+AM=6,
又∵![]() CMP=∠OMC=90°
CMP=∠OMC=90°
∴PC=![]() =4
=4![]()
∵OC=4,PO=8,
∴PC![]() +OC
+OC![]() =PO
=PO![]()
∴∠PCO=90°
∴PC与☉O相切

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目