题目内容
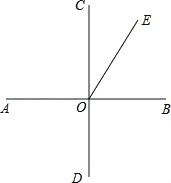
【题目】如图,AB垂直CD(即∠AOC=∠AOD=∠BOD=∠BOC=90°)
(1)比较∠AOD,∠EOB,∠AOE大小(用“<”连接)
(2)如∠EOC=28°,求∠EOB和∠EOD的度数(适当写出解题过程)
【答案】(1)∠EOB<∠AOD<∠AOE;(2)∠EOB=62°;∠EOD=152°.
【解析】
(1)根据已知得出∠AOD=90°,∠EOB<90°,∠AOE>90°,即可得出答案;
(2)代入∠EOB=∠BOC-∠EOC求出即可;代入∠EOD=∠BOD+∠BOE求出即可.
解:(1)∵∠AOC=∠AOD=∠BOD=∠BOC=90°,
∴∠AOD=90°,∠EOB<90°,∠AOE>90°,
即∠EOB<∠AOD<∠AOE.
(2)∵∠EOC=28°,∠BOC=90°,
∴∠EOB=90°﹣28°=62°,
∵∠BOD=90°,
∴∠EOD=∠EOB+∠BOD=62°+90°=152°.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目