题目内容
【题目】已知二次函数![]() 的图象与
的图象与![]() 轴有两个交点
轴有两个交点![]() ,则下列说法正确的有:_________________.(填序号)
,则下列说法正确的有:_________________.(填序号)
①该二次函数的图象一定过定点![]() ;
;
②若该函数图象开口向下,则![]() 的取值范围为:
的取值范围为:![]() ;
;
③当![]() 且
且![]() 时,
时,![]() 的最大值为
的最大值为![]() ;
;
④当![]() 且该函数图象与
且该函数图象与![]() 轴两交点的横坐标
轴两交点的横坐标![]() 满足
满足![]() 时,
时,![]() 的取值范围为:
的取值范围为:![]() .
.
【答案】![]()
【解析】
根据二次函数图象与x轴有两个交点,利用根的判别式可求出![]() ,①中将点代入即可判断,②中根据“开口向下”和“与x轴有两个交点”即可得出m的取值范围,③中根据m的取值可判断出开口方向和对称轴范围,从而判断增减性确定最大值,④中根据开口方向及x1,x2的范围可判断出对应y的取值,从而建立不等式组求解集.
,①中将点代入即可判断,②中根据“开口向下”和“与x轴有两个交点”即可得出m的取值范围,③中根据m的取值可判断出开口方向和对称轴范围,从而判断增减性确定最大值,④中根据开口方向及x1,x2的范围可判断出对应y的取值,从而建立不等式组求解集.
由题目中![]() 可知:
可知:![]() ,
,![]() ,
,![]() ,
,
由题意二次函数图象与x轴有两个交点,则:
![]() ,即
,即![]() ,
,
①将![]() 代入二次函数解析式中,
代入二次函数解析式中,![]() ,则点
,则点![]() 在函数图象上,故正确;
在函数图象上,故正确;
②若二次函数开口向下,则![]() ,解得
,解得![]() ,且
,且![]() ,所以
,所以![]() 的取值范围为:
的取值范围为:![]() ,故正确;
,故正确;
③当![]() 时,
时,![]() ,即二次函数开口向上,对称轴
,即二次函数开口向上,对称轴![]() ,对称轴在
,对称轴在![]() 左侧,则当
左侧,则当![]() 时,
时,![]() 随
随![]() 的增大而增大,当
的增大而增大,当![]() 时有最大值,
时有最大值,![]() ,故错误;
,故错误;
④当![]() 时,
时,![]() ,即二次函数开口向上,
,即二次函数开口向上,
∵![]() ,
,
∴当![]() 时,
时,![]() ,
,![]() 时,
时,![]() ,即
,即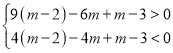 ,
,
解得:![]() ,
,
∵![]() ,
,
∴当![]() 时,
时,![]() ,
,![]() 时,
时,![]() ,即
,即![]() ,
,
解得:![]() ,
,
综上,![]() ,故正确.
,故正确.
故答案为:①②④.

练习册系列答案
相关题目
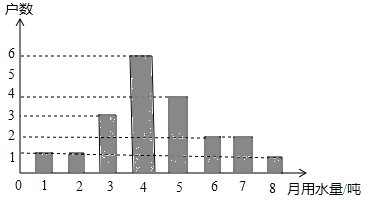
【题目】九(1)班同学为了解某小区家庭月均用水情况(单位:吨),随机调查了该小区部分家庭,并将调查数据进行如下整理:
月均用水量 | 频数(户) | 频率 |
| 6 | 0.12 |
| 0.24 | |
| 16 | 0.32 |
| 10 | 0.20 |
| 4 | |
25 | 2 | 0.04 |
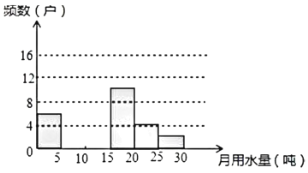
请解答以下问题:
(1)把上面的频数分布表和频数分布直方图补充完整;
(2)若该小区有1000户家庭,根据调查数据估计,该小区月均有水量超过20吨的家庭大约有多少户?