题目内容
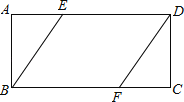
【题目】如图,在![]() ABCD中,对角线AC,BD交于点O,过点B作BE⊥CD于点E,延长CD到点F,使DF=CE,连接AF.
ABCD中,对角线AC,BD交于点O,过点B作BE⊥CD于点E,延长CD到点F,使DF=CE,连接AF.
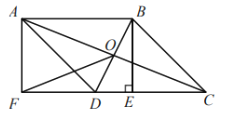
(1)求证:四边形ABEF是矩形;
(2)连接OF,若AB=6,DE=2,∠ADF=45°,求OF的长度.
【答案】(1)见解析;(2) OF =![]() .
.
【解析】
(1)根据菱形的性质得到AD∥BC且AD=BC,等量代换得到BC=EF,推出四边形AEFD是平行四边形,根据矩形的判定定理即可得到结论;
(2)根据直角三角形斜边中线可得:OF=![]() AC,利用勾股定理计算AC的长,可得结论.
AC,利用勾股定理计算AC的长,可得结论.
(1)证明:∵四边形ABCD是平行四边形
∴AB=CD,AB∥CD.
∵DF=CE,
∴DF+DE=CE+ED,
即:FE=CD.
∵点F、E在直线CD上
∴AB=FE,AB∥FE.
∴四边形ABEF是平行四边形
又∵BE⊥CD,垂足是E,
∴∠BEF=90°.
∴四边形ABEF是矩形.
(2)解:∵四边形ABEF是矩形O,
∴∠AFC=90°,AB=FE.
∵AB=6,DE=2,
∴FD=4.
∵FD=CE,
∴CE=4.
∴FC=10.
在Rt△AFD中,∠AFD=90°.
∵∠ADF=45°,
∴AF=FD=4.
在Rt△AFC中,∠AFC=90°.
∴![]() .
.
∵点O是平行四边形ABCD对角线的交点,
∴O为AC中点
在Rt△AFC中,∠AFC=90°.O为AC中点.
∴OF=![]() AC=
AC=![]() .
.

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案【题目】“PM2.5”指数是空气中可入肺颗粒物的含量,是空气质量的指标之一.下表为A市1﹣12月“PM2.5月平均指数”(单位:微克/立方米)
PM2.5指数 | 20 | 30 | 40 | 41 | 43 | 50 |
月数 | 2 | 4 | 3 | 1 | 1 | 1 |
(1)求这12个月“PM2.5月平均指数”的众数、中位数、平均数;
(2)根据《环境空气质量标准》,宜居城市的标准之一是“PM2.5年平均指数少于35微克/立方米”,请你判断A市是否为宜居城市?