题目内容
【题目】如图，在平面直角坐标系中，A、B两点分别在x轴、y轴上，OA=3，OB=4，连接AB．点P在平面内，若以点P、A、B为顶点的三角形与△AOB全等（点P与点O不重合），则点P的坐标为 ．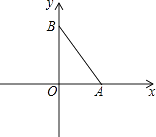 
【答案】（3,4）或（ 
,
）或（﹣ 
,
）
【解析】解：如图所示：①∵OA=3，OB=4，
∴P1（3，4）；②连结OP2，
设AB的解析式为y=kx+b，则
，
解得 
．
故AB的解析式为y=﹣ 
x+4，
则OP2的解析式为y= 
x，
联立方程组得 
，
解得 
，
则P2（ 
， 
）；③连结P2P3，
∵（3+0）÷2=1.5，
（0+4）÷2=2，
∴E（1.5，2），
∵1.5×2﹣ =﹣ 
，
2×2﹣ = 
，
∴P3（﹣ ， ）．
故点P的坐标为（3，4）或（ ， ）或（﹣ ， ）．
所以答案是：（3，4）或（ ， ）或（﹣ ， ）．
练习册系列答案
相关题目
【题目】为了解某校创新能力大赛的笔试情况，随机抽查了部分参赛同学的成绩，整理井制作了不完整的统计表和统计图，请根据图表中提供的信息解答问题：
分数x（分） | 频数 | 百分比 |
60≤x＜70 | 30 | 10% |
70≤x＜80 | 90 | n |
80≤x＜90 | m | 40% |
90≤x＜100 | 60 | 20% |
（1）本次调查统计的学生人数为多少．
（2）在表中：写出m，n的值．
（3）补全频数分布直方图．
