题目内容
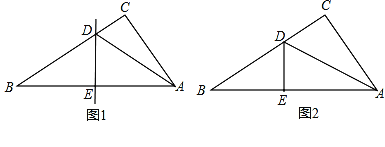
【题目】如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B、C重合),∠ADE=∠B=α,DE交AC于点E,且cosα= ![]() ,则线段CE的最大值为 .
,则线段CE的最大值为 . 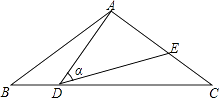
【答案】6.4
【解析】解:作AG⊥BC于G,如图,
∵AB=AC,
∴BG=CG,
∵∠ADE=∠B=α,
∴cosB=cosα= ![]() =
= ![]() ,
,
∴BG= ![]() ×10=8,
×10=8,
∴BC=2BG=16,
设BD=x,则CD=16﹣x,
∵∠ADC=∠B+∠BAD,即α+∠CDE=∠B+∠BAD,
∴∠CDE=∠BAD,
而∠B=∠C,
∴△ABD∽△DCE,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴CE=﹣ ![]() x2+
x2+ ![]() x
x
=﹣ ![]() (x﹣8)2+6.4,
(x﹣8)2+6.4,
当x=8时,CE最大,最大值为6.4.
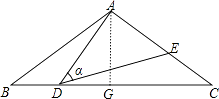
作AG⊥BC于G,如图,根据等腰三角形的性质得BG=CG,再利用余弦的定义计算出BG=8,则BC=2BG=16,设BD=x,则CD=16﹣x,证明△ABD∽△DCE,利用相似比可表示出CE=﹣ ![]() x2+
x2+ ![]() x,然后利用二次函数的性质求CE的最大值.
x,然后利用二次函数的性质求CE的最大值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
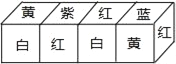
【题目】把正方体的6个面分别涂上不同的颜色,并画上朵数不等的花,各面上的颜色与花朵数的情况如下表:
颜色 | 红 | 黄 | 蓝 | 白 | 紫 | 绿 |
花朵数 | 1 | 2 | 3 | 4 | 5 | 6 |
现将上述大小相同,颜色、花朵分布完全一样的四个正方体拼成一个在同一平面上放置的长方体,如图所示,那么长方体的下底面共有_____朵花.