题目内容
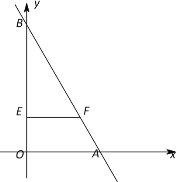
【题目】如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,连接EF、BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC.
(1)求证:OE=OF;
(2)若BC=2 ![]() ,求AB的长.
,求AB的长.
【答案】
(1)证明:在矩形ABCD中,AB∥CD,
∴∠BAC=∠FCO,
在△AOE和△COF中,
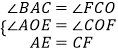 ,
,
∴△AOE≌△COF(AAS),
∴OE=OF
(2)解:如图,连接OB,
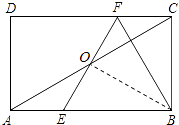
∵BE=BF,OE=OF,
∴BO⊥EF,
∴在Rt△BEO中,∠BEF+∠ABO=90°,
由直角三角形斜边上的中线等于斜边上的一半可知:OA=OB=OC,
∴∠BAC=∠ABO,
又∵∠BEF=2∠BAC,
即2∠BAC+∠BAC=90°,
解得∠BAC=30°,
∵BC=2 ![]() ,
,
∴AC=2BC=4 ![]() ,
,
∴AB= ![]() =
= ![]() =6.
=6.
【解析】(1)依据矩形的性质可知AB∥CD,然后,再根据平行线的性质可得到∠BAC=∠FCO,接下来,利用“AAS”可证明△AOE≌△COF,再根据全等三角形的即可得证;
(2)连接OB,首先依据等腰三角形三线合一的性质可知BO⊥EF,然后再根据矩形的性质可得出OA=OB,接下来,再根据等边对等角的性质证明∠BAC=∠ABO,然后依据三角形的内角和定理可得到∠BAC=30°,在Rt△ABC中,依据含30°直角三角形的性质可求得AC的长,最后,再利用勾股定理可求得AB的长.
【考点精析】根据题目的已知条件,利用等腰三角形的性质和含30度角的直角三角形的相关知识可以得到问题的答案,需要掌握等腰三角形的两个底角相等(简称:等边对等角);在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.

练习册系列答案
相关题目