题目内容
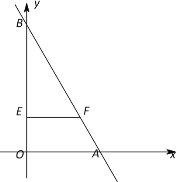
【题目】若直线l1经过点（0，4），l2经过点（3，2），且l1与l2关于x轴对称，则l1与l2的交点坐标为__________．
【答案】
【解析】
根据对称的性质得出两个点关于x轴对称的对称点，再根据待定系数法确定函数关系式，求出一次函数与x轴的交点即可．
∵直线l1经过点（0，4），l2经过点（3，2），且l1与l2关于x轴对称，∴两直线相交于x轴上．
∵直线l1经过点（0，4），l2经过点（3，2），且l1与l2关于x轴对称，∴直线l1经过点（3，﹣2），l2经过点（0，﹣4），把（0，4）和（3，﹣2）代入直线l1经过的解析式y=kx+b，则
，解得：
，故直线l1经过的解析式为：y=﹣2x+4，可得l1与l2的交点坐标为l1与l2与x轴的交点，解得：x=2，即l1与l2的交点坐标为（2，0）．
故答案为：（2，0）．
练习册系列答案
名校课堂系列答案
相关题目
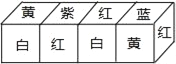
【题目】把正方体的6个面分别涂上不同的颜色，并画上朵数不等的花，各面上的颜色与花朵数的情况如下表：
颜色 | 红 | 黄 | 蓝 | 白 | 紫 | 绿 |
花朵数 | 1 | 2 | 3 | 4 | 5 | 6 |
现将上述大小相同，颜色、花朵分布完全一样的四个正方体拼成一个在同一平面上放置的长方体，如图所示，那么长方体的下底面共有_____朵花．
