Question

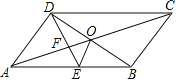
【题目】如图，ABCD的对角线AC、BD交于点O，DE平分∠ADC交AB于点E，∠BCD=60°，AD=AB，连接OE．下列结论：①SABCD=ADBD；②DB平分∠CDE；③AO=DE；④S△ADE=5S△OFE，其中正确的个数有（　　）

A. 1个 B. 2个 C. 3个 D. 4个

Answer 1

【答案】B

【解析】求得∠ADB=90°，即AD⊥BD，即可得到SABCD=ADBD；依据∠CDE=60°，∠BDE30°，可得∠CDB=∠BDE，进而得出DB平分∠CDE；依据Rt△AOD中，AO＞AD，即可得到AO＞DE；依据OE是△ABD的中位线，即可得到OE∥AD，OE=AD，进而得到△OEF∽△ADF，依据S△ADF=4S△OEF，S△AEF=2S△OEF，即可得到S△ADE=6S△OFE．

∵∠BAD=∠BCD=60°，∠ADC=120°，DE平分∠ADC，

∴∠ADE=∠DAE=60°=∠AED，

∴△ADE是等边三角形，

∴AD=AE=AB，

∴E是AB的中点，

∴DE=BE，

∴∠BDE=∠AED=30°，

∴∠ADB=90°，即AD⊥BD，

∴SABCD=ADBD，故①正确；

∵∠CDE=60°，∠BDE30°，

∴∠CDB=∠BDE，

∴DB平分∠CDE，故②正确；

∵Rt△AOD中，AO＞AD，

∴AO＞DE，故③错误；

∵O是BD的中点，E是AB的中点，

∴OE是△ABD的中位线，

∴OE∥AD，OE=AD，

∴△OEF∽△ADF，

∴S△ADF=4S△OEF，且AF=2OF，

∴S△AEF=2S△OEF，

∴S△ADE=6S△OFE，故④错误，

故选B．