题目内容
【题目】已知抛物线![]() 与x轴交于A、B两点
与x轴交于A、B两点![]() 点A在点B的左侧
点A在点B的左侧![]() .
.
![]() 当
当![]() 时,抛物线与y轴交于点C.
时,抛物线与y轴交于点C.
![]() 直接写出点A、B、C的坐标;
直接写出点A、B、C的坐标;
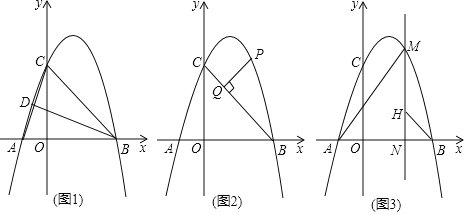
![]() 如图1,连接AC,在x轴上方的抛物线上有一点D,若
如图1,连接AC,在x轴上方的抛物线上有一点D,若![]() ,求点D的坐标;
,求点D的坐标;
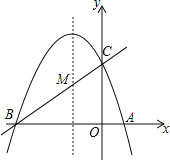
![]() 如图2,点P为抛物线位于第一象限图象上一动点,过P作
如图2,点P为抛物线位于第一象限图象上一动点,过P作![]() ,求PQ的最大值;
,求PQ的最大值;
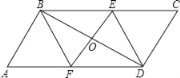
![]() 如图3,若点M为抛物线位于x轴上方图象上一动点,过点M作
如图3,若点M为抛物线位于x轴上方图象上一动点,过点M作![]() 轴,垂足为N,直线MN上有一点H,满足
轴,垂足为N,直线MN上有一点H,满足![]() 与
与![]() 互余,试判断HN的长是否变化,若变化,请说明理由,若不变,请求出HN长.
互余,试判断HN的长是否变化,若变化,请说明理由,若不变,请求出HN长.
【答案】(1)①A(-1,0),B(3,0),C(0,3)②D点坐标为(![]() ,
,![]() )③PQ最大为
)③PQ最大为![]() (2)NH=1为定值,故不变.
(2)NH=1为定值,故不变.
【解析】
(1)①将m带入抛物线解析式解得与x,y轴的交点.
②设OC交BD于点E,过D点作x轴垂线交x轴F点, 利用△EOB∽△DFB,求得D点的纵坐标,在代入AC的直线方程即可.
③求PQ的最大值,即求△BCP面积的最大值,列出其面积最大值的二次函数配方式计算.
(2)运用△MAN∽△BHN,得到NH的值即可.
(1)![]() 当m=2时,
当m=2时,![]() 为
为![]() ,当x=0时,y=3
,当x=0时,y=3
当y=0时,x=-1或x=3.
综上,A(-1,0),B(3,0),C(0,3)
②
设OC交BD于点E,过D点作x轴垂线交x轴F点.
由①知,AB=4,OC=3
∴AC=![]() ,BD=
,BD=![]()
∵![]() ,OB=OC,∠AOC=∠EOB
,OB=OC,∠AOC=∠EOB
∴△AOC≌△EOB(ASA)
∴OE=1
∵△EOB∽△DFB
∴![]()
DF=![]() ,即D点坐标为
,即D点坐标为![]()
带入直线AC中得D点横坐标为![]() .
.
故D点坐标为(![]() ,
,![]() )
)
③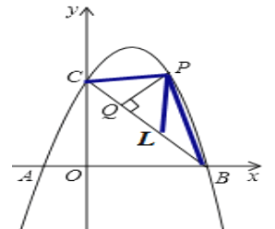
求PQ的最大值,即求△BCP面积的最大值,过P点作PL∥y轴,交BC于点L
设P点坐标为(x,![]() ),则L为(x,-x+3)
),则L为(x,-x+3)
则S△BCP=![]() ·PL·3=
·PL·3=![]() ·(
·(![]() )= -
)= -![]() ·
·![]()
∴当x=![]() 时,S△BCP最大为
时,S△BCP最大为![]() .
.
此时PQ最大为![]() .
.
(2)设N点为x,则AN=1+x,BN=3-x,MN=![]()
∵![]() 与
与![]() 互余,∠MNA=∠BNH=90°
互余,∠MNA=∠BNH=90°
∴△MAN∽△BHN
∴![]() ,即
,即![]()
∴NH=1为定值,故不变.

【题目】为了传承中华优秀传统文化,某校组织了一次八年级350名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中若干名学生的成绩(成绩![]() 取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
成绩x/分 | 频数 | 频率 |
50≤x<60 | 2 | 0.04 |
60≤x<70 | 6 | 0.12 |
70≤x<80 | 9 |
|
80≤x<90 | 0.36 | |
90≤x≤100 | 15 | 0.30 |

请根据所给信息,解答下列问题:
(1)a等于多少,b等于多少;
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数会落在哪个分数段;
(4)若成绩在90分以上(包括90分)的为“优”等,则该年级参加这次比赛的350名学生中成绩“优”等的约有多少人?