Question

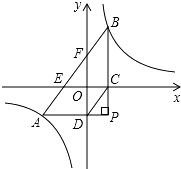
【题目】如图，将透明三角形纸片PAB的直角顶点P落在第四象限，顶点A、B分别落在反比例函数y= 图象的两支上，且PB⊥x于点C，PA⊥y于点D，AB分别与x轴，y轴相交于点E、F．已知B（1，3）．

（1）k=；
（2）试说明AE=BF；
（3）当四边形ABCD的面积为 时，求点P的坐标．

Answer 1

【答案】
（1）3
（2）

解：反比例函数解析式为y= ，

设A点坐标为（a， ），

∵PB⊥x于点C，PA⊥y于点D，

∴D点坐标为（0， ），P点坐标为（1， ），C点坐标为（1，0），

∴PB=3﹣ ，PC=﹣ ，PA=1﹣a，PD=1，

∴ = = ， = ，

∴ = ，

而∠CPD=∠BPA，

∴△PCD∽△PBA，

∴∠PCD=∠PBA，

∴CD∥BA，

而BC∥DF，AD∥EC，

∴四边形BCDF、ADCE都是平行四边形，

∴BF=CD，AE=CD，

∴BF=AE，

（3）

解：∵四边形ABCD的面积=S△PAB﹣S△PCD，

∴ （3﹣ ）（1﹣a）﹣ 1（﹣ ）= ，

整理得a+ =0，解得a=﹣ ，

∴P点坐标为（1，﹣2）．

【解析】解：（1）把B（1，3）代入y= 得k=1×3=3；
故答案为：3；
（1）根据反比例函数图象上点的坐标特征易得k=3；（2）设A点坐标为（a， ），易得D点坐标为（0， ），P点坐标为（1， ），C点坐标为（1，0），根据图形与坐标的关系得到PB=3﹣ ，PC=﹣ ，PA=1﹣a，PD=1，则可计算出 = = ，加上∠CPD=∠BPA，根据相似的判定得到△PCD∽△PBA，则∠PCD=∠PBA，于是判断CD∥BA，根据平行四边形的判定方法易得四边形BCDF、ADCE都是平行四边形，所以BF=CD，AE=CD，则BF=AE，于是有AE=BF；（3）利用四边形ABCD的面积=S△PAB﹣S△PCD ， 和三角形面积公式得到 （3﹣ ）（1﹣a）﹣ 1（﹣ ）= ，整理得a+ =0，然后解方程求出a的值，再写出P点坐标．