��Ŀ����
����Ŀ����ͼ�٣���ƽ��ֱ������ϵ�У�һ�����ֱ�����ǰ�ABC��ֱ�Ƕ���A��y���ϣ�����Ϊ��0����1������һ����B����Ϊ����2��0������֪���κ���y= ![]() x2+bx+c��ͼ��B��C���㣮�ֽ�һ��ֱ�߷�����ֱ������ϵ�У�ʹֱ�ߵı�A��D���y���Ҿ�����B��ֱ����x��������ƽ�ƣ���A��D����y���غ�ʱ�˶�ֹͣ��
x2+bx+c��ͼ��B��C���㣮�ֽ�һ��ֱ�߷�����ֱ������ϵ�У�ʹֱ�ߵı�A��D���y���Ҿ�����B��ֱ����x��������ƽ�ƣ���A��D����y���غ�ʱ�˶�ֹͣ��
��1�����C�����꼰���κ����Ĺ�ϵʽ��
��2�����˶�������ֱ�ߵı�A��D�佻��BC�ڵ�M�����������ڵ�N�����߶�MN���ȵ����ֵ��
��3����ͼ�ڣ����PΪֱ�ߵı�A��D���ϵ���һ�㣬����PA��PB��PC��QΪBC���е㣬��̽������ֱ��ƽ�ƵĹ����У���PQ= ![]() ʱ���߶�PA��PB��PC֮���������ϵ����ֱ��д�����ۣ���ָ����Ӧ�ĵ�P�������ߵ�λ�ù�ϵ��
ʱ���߶�PA��PB��PC֮���������ϵ����ֱ��д�����ۣ���ָ����Ӧ�ĵ�P�������ߵ�λ�ù�ϵ��
��˵�������������ߵ�λ�ù�ϵ�ɷ�Ϊ���࣬���磬ͼ���У���A���������ڣ���C���������ϣ���D�����������⣮��

���𰸡�
��1��
��ͼ1������C��CD��y����D����ʱ��CDA�ա�AOB��

�ߡ�CDA�ա�AOB��
��AD=BO=2��CD=AO=1��
��OD=OA+AD=3��
��C����1����3����
��B����2��0����C����1����3������������y= ![]() x2+bx+c��
x2+bx+c��
��� b= ![]() ��c=��3��
��c=��3��
�������ߵĽ���ʽΪy= ![]() x2+
x2+ ![]() x��3��
x��3��
��2��
��lBC��y=kx+b��
��B����2��0����C����1����3����
�� ![]() ��
��
��� ![]() ��
��
��lBC��y=��3x��6��
��M��xM����3xM��6����N��xN�� ![]() xN2+
xN2+ ![]() xN��3����
xN��3����
��xM=xN����Ϊx����yM��yN��
���߶�MN����=��3x��6���� ![]() x2+
x2+ ![]() x��3��=��
x��3��=�� ![]() ��x+
��x+ ![]() ��2+
��2+ ![]() ������2��x�ܩ�1����
������2��x�ܩ�1����
�൱x=�� ![]() ʱ���߶�MN����Ϊ���ֵ
ʱ���߶�MN����Ϊ���ֵ ![]() ��
��
��3��
��P����������ʱ��BP+CP= ![]() AP��P����������ʱ��BP+CP=
AP��P����������ʱ��BP+CP= ![]() AP��P���������ڣ�PC��PB=
AP��P���������ڣ�PC��PB= ![]() PA��
PA��
�������£�
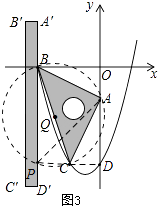
��ͼ2����Q��ΪԲ�ģ� ![]() Ϊ�뾶����Q��
Ϊ�뾶����Q��

��OB=2��OA=1��
��AC=AB= ![]() =
= ![]() ��
��
��BC= ![]() =
= ![]() ��
��
��BQ=CQ= ![]() ��
��
�ߡ�BAC=90�㣬
���B��A��C���ڡ�Q�ϣ�
��P���������⣬
��ͼ3��ԲQ��BD��Ľ��㼴Ϊ��P������PB��PC��PA���ӳ�PC��y���ڵ�D
��BCΪֱ����
���BPC=90��
��BD����y��ƽ��
���ADC=90�㣬��D��Ϊ��������y�ύ��
��PD��x��
��PC=1��PB=3��PA=2 ![]()
��BP+CP= ![]() AP��
AP��
��P���������ϣ���ʱ��Pֻ��ΪB�����C�㣬
��AC=AB= ![]() ��
��
��AP= ![]() ��
��
��BP+CP=BC= ![]() ��
��
��BP+CP= ![]() AP��
AP��
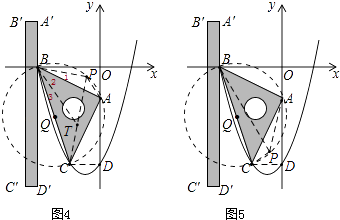
��P���������ڣ��������������ͼ4��5��
��ͼ4����PC��ȡBP=PT��
��BCΪֱ����
���BPC=90��
���BPTΪ����ֱ��������
���PBT=45��=��1+��2
�ߡ�ABC=��3+��2=45��
���1=��3
�ߡ�BAP=��BCP��ͬ��BP��
���BPA�ס�BTC
�� ![]()
��PC=PT+CT
��PC=PT+ ![]() PA=PB+
PA=PB+ ![]() PA
PA
��PC��PB= ![]() PA
PA
ͬ������ͼ5��Ҳ�ɵ�PB��PC= ![]() PA��
PA��
����������1����C�����꣬������x��y�ᴹ�ߣ���ʾ�������꣬�á�CDA�ա�AOB������C��������֪�����������߽���ʽ�ã���2����������ͬ��������룬������������������������Ϊ����ֱ���ֱ��BC���������ϣ��ʿ������ý���ʽ���������Ϊx����ʾ���������꣮����ǵù���x�Ķ��κ�����������ֵ���ʣ��������3�������ã�BC= ![]() ����ΪQΪBC���е㣬PQ=
����ΪQΪBC���е㣬PQ= ![]() ǡΪ�뾶��������Բ��P�����Բ�ϣ�������������н��
ǡΪ�뾶��������Բ��P�����Բ�ϣ�������������н��
�����㾫����������Ҫ�����˶��κ��������ʵ����֪ʶ�㣬��Ҫ���������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С������ȷ�����⣮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�




